Cho tam giác ABC có ba góc nhọn, $\hat{A}={60}^\circ$. Điểm $M\in BC$. Hạ ME $\bot$ AB, MF $\bot$ AC. Gọi I là trung điểm AM.
a)Tính góc $\widehat{EIF}$;
b) Tính $EF$ nếu $AM = a (a > 0)$;
c) Tìm vị trí điểm M để độ dài đoạn EF nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AEM=góc AFM=90 độ
=>AEMF là tứ giác nội tiếp đường tròn đường kính AM
=>AEMF nội tiếp (I)
Xét (I) có
góc EIF là góc ở tâm chắn cung EF
góc EAF là góc nội tiếp chắn cung EF
Do đó: góc EIF=2*góc EAF=120 độ không đổi
b: Xét ΔEIF có IE=IF
nên ΔIEF cân tại I
=>góc IEF=(180-120)/2=30 độ
Xét ΔIEF có \(\dfrac{IF}{sinIEF}=\dfrac{EF}{sinEIF}\)
=>\(\dfrac{IF}{sin30}=\dfrac{EF}{sin120}\)
=>\(EF=\dfrac{IF}{sin30}\cdot sin120=\dfrac{AM}{2}\cdot\sqrt{3}=AM\cdot\dfrac{\sqrt{3}}{2}\)

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

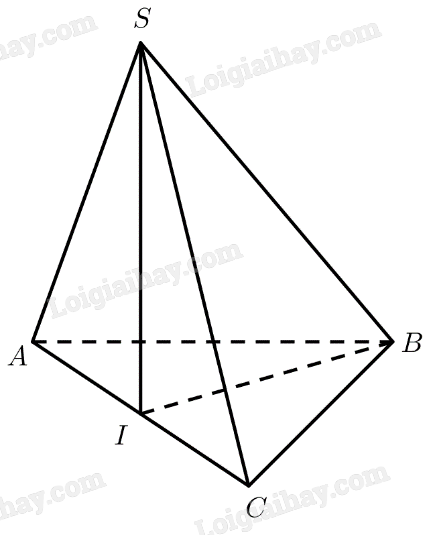
Xét tam giác \(SAC\) có:
\(AC = \sqrt {S{A^2} + S{C^2} - 2.SA.SC.\cos \widehat {ASC}} = a\sqrt 3 \)
\(SI\) là trung tuyến \( \Rightarrow SI = \frac{{\sqrt {2\left( {S{A^2} + S{C^2}} \right) - A{C^2}} }}{2} = \frac{a}{2}\)
Ta có: \(S{I^2} + A{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{A^2}\)
\( \Rightarrow \Delta SAI\) vuông tại \(I \Rightarrow SI \bot AC\)
Xét tam giác \(SAB\) vuông tại \(S\) có: \(AB = \sqrt {S{A^2} + S{B^2}} = a\sqrt 2 \)
Xét tam giác \(SBC\) cân tại \(S\) có \(\widehat {BSC} = {60^ \circ }\) nên tam giác \(SBC\) đều. Vậy \(BC = a\)
Xét tam giác \(ABC\) có: \(A{B^2} + B{C^2} = {\left( {a\sqrt 2 } \right)^2} + {a^2} = 3{a^2} = A{C^2}\)
\( \Rightarrow \Delta ABC\) vuông tại \(B \Rightarrow BI = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(SBI\) có: \(S{I^2} + B{I^2} = {\left( {\frac{a}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {a^2} = S{B^2}\)
\( \Rightarrow \Delta SBI\) vuông tại \(I \Rightarrow SI \bot BI\)
Ta có:
\(\left. \begin{array}{l}SI \bot AC\\SI \bot BI\end{array} \right\} \Rightarrow SI \bot \left( {ABC} \right)\)

Bài làm:
Ta có: Vì ΔABC đều => \(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
Xét Δ vuông MBE có BE = 1/2 BM
=> \(EM^2=BM^2-BE^2=BM^2-\frac{1}{4}BM^2=\frac{3}{4}BM^2\)
=> \(EM=\frac{BM\sqrt{3}}{2}\)
Tương tự CM được: \(FM=\frac{MC\sqrt{3}}{2}\)
=> \(ME+MF=\frac{\left(BM+MC\right)\sqrt{3}}{2}=\frac{BC.\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)\)
b) Ta có: Theo tính chất đường trung tuyến ứng với cạnh huyền
=> \(IE=FI=\frac{AM}{2}=AI\)
Vì IE = AI => Δ AIE cân tại I => \(\widehat{IAE}=\widehat{IEA}\)
=> \(\widehat{EIM}=\widehat{IAE}+\widehat{IEA}=2\widehat{IAE}\)
Tương tự CM được: \(\widehat{FIM}=2\widehat{FAI}\)
=> \(\widehat{EIM}+\widehat{FIM}=2\left(\widehat{IAE}+\widehat{FAI}\right)=2.60^0=120^0\)
=>\(\widehat{EIF}=120^0\)
c) Khi AM = 20cm => \(EI=FI=10cm\)
=> Δ EIF cân tại I => \(\widehat{FEI}=\widehat{IFE}=30^0\)
Xong từ I kẻ đường cao xuống EF làm 1 vài động tác CM ra được: \(EF=10\sqrt{3}cm\)
(ko hiểu thì ib)
d) Áp dụng t/c đường xiên hình chiếu => Min AM = AH khi M trùng H

a) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \tan {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{\sqrt 3 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {SMA} = \arctan \frac{1}{2}\)
DE ngắn nhất ⇔ AM ngắn nhất. Điều đó xảy ra khi AM là đường cao ΔABC.
a) Vì \widehat{AEM}=\widehat{AFM}={90}^\circAEM=AFM=90∘ nên A, E, M, F thuộc đường tròn tâm I đường kính AM \Rightarrow\ \widehat{EIF}=2\widehat{EAF}={120}^\circ⇒ EIF=2EAF=120∘ (góc ở tâm bằng hai lần góc nội tiếp chắn cung \stackrel\frown{EF}EF⌢).
b) Hạ IH\bot EFIH⊥EF, ta có IE=IF=\frac{1}{2}AMIE=IF=21AM nên \Delta IEFΔIEF cân \Rightarrow HE=HF⇒HE=HF.
Ta lại có: EH=EI.\sin{\widehat{EIH}}=\frac{1}{2}AM.\sin{{60}^\circ}EH=EI.sinEIH=21AM.sin60∘ (vì \widehat{EIH}=\widehat{FIH}=\frac{1}{2}\widehat{EIF}={60}^\circEIH=FIH=21EIF=60∘).
Suy ra EH=\frac{a}{2}.\frac{\sqrt3}{2}=\frac{a\sqrt3}{4}\Rightarrow EF=2EH=\frac{a\sqrt3}{2}EH=2a.23=4a3⇒EF=2EH=2a3.
c) EF nhỏ nhất khi AM nhỏ nhất \Leftrightarrow⇔ AM \bot⊥ BC.