Cho hình bình hành ABCD. Gọi E, F tương ứng là trung điểm của CD và AB.
A) Chứng minh rằng AECF là một hình bình hành;
b) AE cắt BD tại I, còn CF cắt BD tại H. Chứng minh rằng DI=IH=HB.
c) Gọi J là giao điểm của BE với CF. Chứng minh rằng 4HJ=HC
Giúp mình mới nhoa.Mình xin chân thành cảm ơn...
Đọc tiếp
Cho hình bình hành ABCD. Gọi E, F tương ứng là trung điểm của CD và AB.
A) Chứng minh rằng AECF là một hình bình hành;
b) AE cắt BD tại I, còn CF cắt BD tại H. Chứng minh rằng DI=IH=HB.
c) Gọi J là giao điểm của BE với CF. Chứng minh rằng 4HJ=HC
Giúp mình mới nhoa
.Mình xin chân thành cảm ơn 
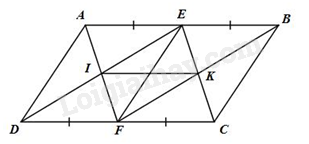
Xét hbh ABCD có :
AB = CD; AB // CD
Mà e là trg điểm của AB, E là trg điểm của CD
=> AF//EC, AF=EC
=> Tứ giác AFEC là hbh
b/ Xét tam giác DHC có:
IE//HC( hbh AFEC)
E là trg điểm của DC
=> I là trg điểm của DH (1)
chứng minh tương tự tam giác AIB
=> H là trg điểm của IB (2)
Từ (1) và (2) => đpcm
c/Xét tam giác DHC có:
I là ttrg điểm của DH
E là trg điểm của DC
=> IE là đg trbình của tg DHC
=> IE= 1/2 HC (3)
Xeý tg IEB có:
H là trg điểm của IB
HJ // IE (AE// FC; J thuộc FC)
=> J là trung điểm của BE
=> HJ là đg trbình của tg BIE
=> HJ = 1/2 IE (4)
Từ (3) và (4) => HJ = 1/4 HC hay 4HJ = HC