Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;−3;1), B(1;2;0)và )M(a;0;b) sao cho P=|MA→−2MB→| đạt giá trị nhỏ nhất. Khi đó a+2b bằng...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;−3;1), B(1;2;0)và )M(a;0;b) sao cho P=|MA→−2MB→| đạt giá trị nhỏ nhất. Khi đó a+2b bằng :
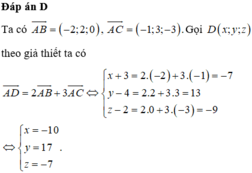
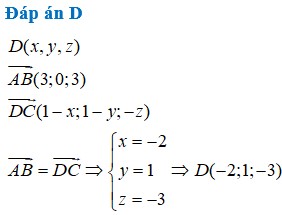
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(a-2;3;b-1\right)\\\overrightarrow{MB}=\left(a-1;-2;b\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}-2\overrightarrow{MB}=\left(-a;7;-b-1\right)\)
\(\Rightarrow\left|\overrightarrow{MA}-2\overrightarrow{MB}\right|=\sqrt{a^2+\left(b+1\right)^2+7^2}\ge7\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=0\\b=-1\end{matrix}\right.\) \(\Rightarrow a+2b=-2\)