Cho 3 điểm A(-6;3) B(0;-1) C(3;2) . M(a;b) là điểm nằm trên d: 2x -y +3=0 sao cho \(|\)\(\overrightarrow{Ma}+\overrightarrow{MB}+\overrightarrow{MC}\)\(_|\) nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hình vẽ: A B C D E F
Có hình vẽ như vậy là đơn giản rồi! Tự làm nhé

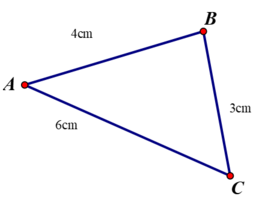
a) Ta có: AB + BC = 4 +3 = 7 (cm), AC = 6 cm.
Nên AB + BC ≠ AC. Vậy điểm B không nằm giữa A, C.
Ta có: AB + AC = 4 + 6 = 10 (cm), BC = 3 cm.
Nên AB + AC ≠ BC. Vậy điểm A không nằm giữa B, C.
Ta có: AC + BC = 6 + 3 = 9 (cm), AB = 4 cm.
Nên AC + BC ≠ AB. Vậy điểm C không nằm giữa A, B.
Do \(M\in d\Rightarrow M\left(a;2a+3\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-6-a;-2a\right)\\\overrightarrow{MB}=\left(-a;-4-2a\right)\\\overrightarrow{MC}=\left(3-a;-1-2a\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\left(-3-3a;-5-6a\right)\)
\(\Rightarrow P=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\sqrt{\left(3a+3\right)^2+\left(6a+5\right)^2}\)
\(\Rightarrow P=\sqrt{45a^2+78a+34}=\sqrt{45\left(a+\frac{13}{15}\right)^2+\frac{1}{5}}\ge\sqrt{\frac{1}{5}}\)
\(\Rightarrow P_{min}=\frac{1}{\sqrt{5}}\) khi \(a=-\frac{13}{15}\Rightarrow M\left(-\frac{13}{15};\frac{19}{15}\right)\)