Cho hình chóp S.ABC có mặt phẳng (SAC) vuông góc với đáy (ABC); SA = AB = a, AC = 2a và A S C ^ = A B C ^ = 90 0 . Tính theo a thể tích khối chóp S.ABC.
A . a 3 2 4
B . 3 a 3 4
C . a 3 4
D . a 3 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
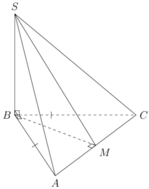
Gọi M là trung điểm của AC thì góc của (SAC) và (BAC) bằng S M B ^ = 60 °
Ta có: tam giác ABC vuông cân tại B nên
B M = 1 2 A C = a 2 2 ⇒ S A B C = 1 2 B M . A C = 1 2 . a 2 2 . a 2 = a 2 2
Mặt khác, S B = B M . tan 60 ° = a 6 2
Vậy V = 1 3 . a 2 2 . a 6 2 = a 3 6 12

Đáp án C
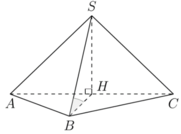
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12

Gọi H, J lần lượt là trung điểm của BC, AC.
Ta có : \(\begin{cases}SH\perp\left(ABC\right)\\HJ\perp AC\end{cases}\) \(\Rightarrow AC\perp SJ\)=> SJH = 60 độ
\(AB=\frac{BC}{\sqrt{2}}=a\sqrt{2};HJ=\frac{AB}{2}=\frac{\sqrt{2a}}{2};SH=HJ.\tan60^o=\frac{a\sqrt{6}}{2}\)
Ta có : \(V_{S.ABC}=\frac{1}{3}SH\frac{AB.AC}{2}=\frac{1}{6}.\frac{\sqrt{6}}{2}.\left(\sqrt{2}\right)^2.a^3=\frac{a^3\sqrt{6}}{6}\)
Gọi E là hình chiếu của H lên SJ, khi đó ta có \(\begin{cases}HE\perp SJ\\HE\perp AC\end{cases}\) \(\Rightarrow HE\perp\left(SAC\right)\)
Mặt khác, do IH SC IH SAC / / (SAC) , suy ra
\(d\left[I,\left(SAC\right)\right]=d\left[H,\left(SAC\right)\right]=HE=HJ.\sin60^o=\frac{\sqrt{6}}{4}a\)
Đáp án C.
Kẻ SH ⊥ AC, do (SAC) ⊥ (ABC)=> SH ⊥ (ABC)
Có BC =