Cho mạch điện như hình vẽ R1= 2R3= 4R4= 40 Ohm; R2= 30 Ohm. Tính điện trở tương đương của đoạn mạch trong trường hợp:
a) Khi K1 đóng, K2 ngắt.
b) Khi K1 ngắt, K2 đóng.
c) Khi K1, K2 đều đóng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
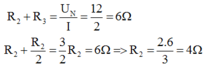
Điện trở của mạch: 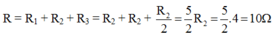
Vậy U = I.R = 2.10 = 20V
→ Đáp án C

Đáp án C
Điện trở của: R 2 + R 3 = U N / I = 12 / 2 = 6 ( Ω )
R 2 + R 2 / 2 = 3 / 2 R 2 = 6 ( Ω ) ⇔ R 2 = 2 . 6 / 3 = 4 ( Ω )
Điện trở của mạch: R = R 1 + R 2 + R 3 = R 2 + R 2 + R 2 / 2 = 10 ( Ω ) .
Vậy U = I.R = 2.10 = 20(V)

\(=>R1nt\left[\left(R2ntR3\right)//R4\right]\)
\(=>Rtd=R1+\dfrac{\left(R2+R3\right)R4}{R2+R3+R4}=20+\dfrac{\left(20+10\right)20}{20+10+20}=32\left(ôm\right)\)
\(=>Im=\dfrac{U}{Rtd}=\dfrac{72}{32}=2,25A=I1=I234\)
\(=>U1=Uac=I1.R1=2,25.20=45V\)
chắc là tính Ubc chứ nhỉ, vì có Uab rồi mà bạn
\(=>Ubc=Uab-Uac=72-45=27V\)

Đáp án B.
Điện trở mạch ngoài
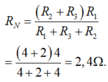
Theo định luật Ôm cho toàn mạch:


Khi hệ ổn định, năng lượng của tụ điện là:
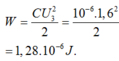
Khi ngắt nguồn, tụ điện phóng điện qua các điện trở, năng lượng dự trữ trong tụ giải phóng dưới dạng nhiệt tỏa ra trên điện trở, với:
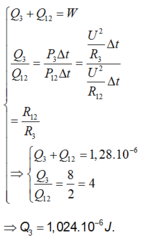

\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{4.12}{4+12}=3\left(\Omega\right)\)
\(U=U_1=U_2=I.R_{tđ}=2.3=6\left(V\right)\)
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{6}{4}=\dfrac{3}{2}\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{6}{12}=\dfrac{1}{2}\left(A\right)\end{matrix}\right.\)