co đường tròn (O;R) và điểm S sao cho SO=2R . vẽ các tiếp tuyến SA, SB của đường tròn (O;R) (A,B là các tiếp điểm ) , và cát tuyến SMN ( không qua O) . gọi I là trung điểm của MN.
a/ chứng minh 5 điểm S,A,O,I,B cùng thuộc moottj đường tròn
b/ chứng minh SA2 = SM.SN
c/ tính SM và SN theo R khi MN= SA
d/ kẻ MH⊥OA , MH cát AN, AB tại D và E . chứng minh tứ giác IEMB nội tiếp đường tròn
e/ tính chu vi và diện tích hnhf phẳng giới hạn bởi SA, SB và cung AB
HELP ME !!!!!!!!!

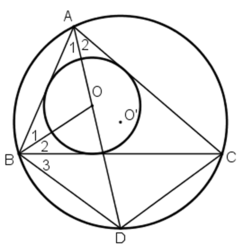

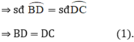
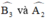 đều là các góc nội tiếp chắn
đều là các góc nội tiếp chắn 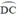
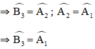
 là góc ngoài của tam giác
là góc ngoài của tam giác

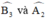 đều là các góc nội tiếp chắn
đều là các góc nội tiếp chắn 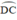
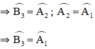
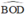 là góc ngoài của tam giác
là góc ngoài của tam giác


a: Xét tứ giác SAOB có \(\widehat{SAO}+\widehat{SBO}=180^0\)
nên SAOB là tứ giác nội tiếp
=>S,A,O,B cùng thuộc 1 đường tròn(1)
Xét tứ giác SIOB có \(\widehat{SIO}+\widehat{SBO}=180^0\)
nên SIOB là tứ giác nội tiếp
=>S,I,O,B cùng thuộc 1 đường tròn(2)
Từ (1) và (2) suy ra S,O,A,B,I cùng thuộc một đường tròn
b: Xét ΔSAM và ΔSNA có
\(\widehat{SAM}=\widehat{SNA}\)
\(\widehat{ASM}\) chung
Do đó: ΔSAM\(\sim\)ΔSNA
Suy ra: SA/SN=SM/SA
hay \(SA^2=SN\cdot SM\)