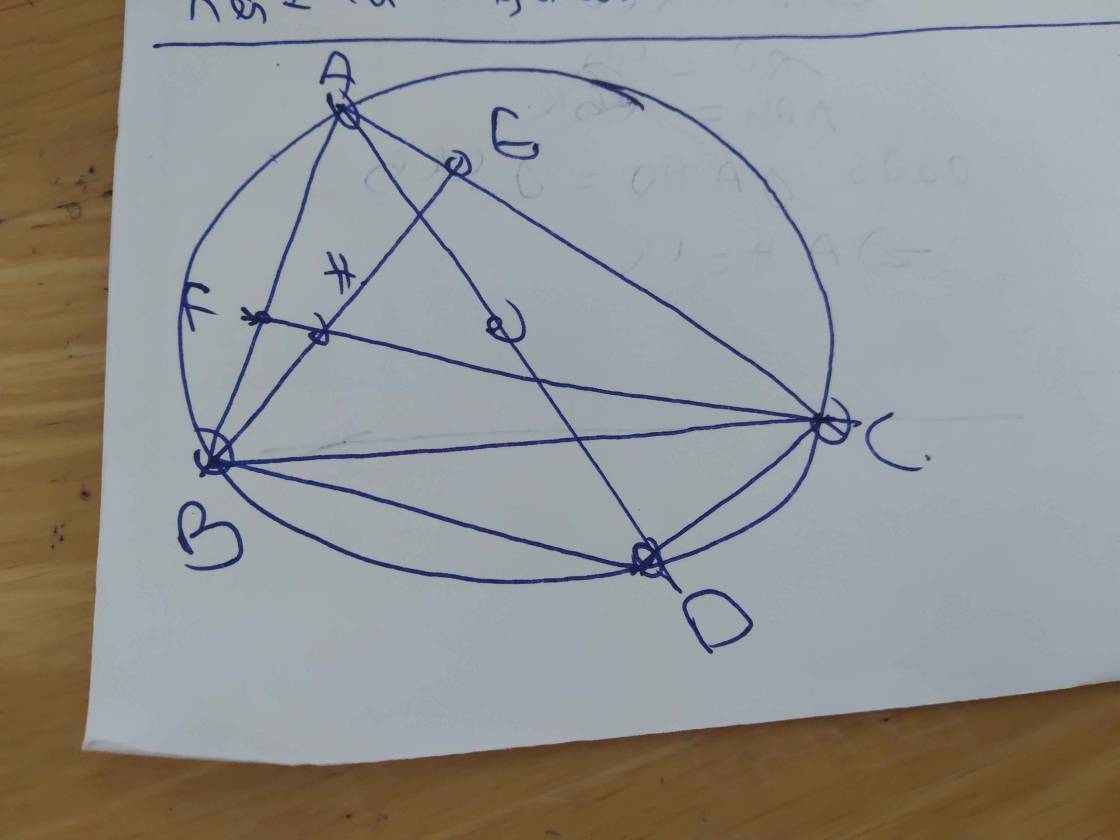
1) Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). Các đường cao AD, BE, CF đồng quy tại H. Gọi M là trung điểm của BC. Chứng minh rằng:
a) AH=2.OM
b) Gọi S và p lần lượt là diện tích và chu vi của tam giác ABC. Chứng minh rằng: 2S\(\geq\)pR. Dấu "=" xảy ra khi nào?
2) Cho nửa đường tròn (O;R), đường kính AB, dây CD song song với AB (D thuộc cung AC). Đặt độ dài dây CD là x (0<x<2R); Diện tích tứ giác ABCD là y.
a) Tính y theo R và x.
b) Tìm GTLN của y theo R.
3) Cho (O;R), đường kính AB. Dây CD quay xung quanh trung điểm M của đoạn OB. Các tia CO và DO lần lượt cắt AD và AC tương ứng ở E và F. Xác định vị trí của dây CD để CE.DF đạt GTNN, tính GTNN đó theo R/