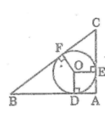
Cho tam giác ABC vuông tại A nội tiếp đường tròn (O;R) có đường kính BC và cạnh AB=R. Kẻ dây AD vuông góc với BC tại H
a) Tính độ dài các cạnh AC,AH và số đo góc B, góc C
b) Chứng minh: AH.HD=HB.HC
c) Gọi M là giao điểm của AC và BD. Qua M kẻ đường thẳng vuông góc với BC cắt BC ở I, căt AC ở N. Chứng minh: C,D,N thẳng hàng
d) Chứng minh: AI là tiếp tuyến của đường tròn (O) và tính AI theo R

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=\left(2\cdot R\right)^2-R^2=3\cdot R^2\)
\(\Leftrightarrow AC=R\cdot\sqrt{3}\)(đvđd)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot2R=R\cdot R\sqrt{3}\)
hay \(AH=\dfrac{R\sqrt{3}}{2}\)(đvđd)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{R\sqrt{3}}{2\cdot R}=\dfrac{\sqrt{3}}{2}\)
hay \(\widehat{ABC}=60^0\)
Xét ΔABC vuông tại A có
\(\widehat{ABC}+\widehat{ACB}=90^0\)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(AC=R\cdot\sqrt{3}\) đvđd; \(AH=\dfrac{R\sqrt{3}}{2}\)đvđd; \(\widehat{ABC}=60^0\); \(\widehat{ACB}=30^0\)
b) Xét (O) có
BC là đường kính của (O)(gt)
AD là dây của đường tròn(O)
BC⊥AD tại H(gt)
Do đó: H là trung điểm của AD(Định lí đường kính vuông góc với dây)
⇔AH=HD
hay \(AH\cdot HD=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\)(2)
Từ (1) và (2) suy ra \(AH\cdot HD=HB\cdot HC\)(đpcm)