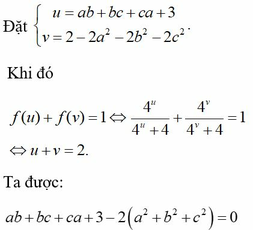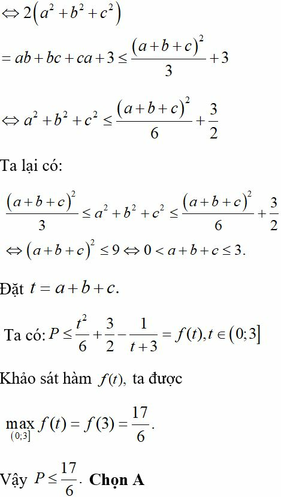.
Bài 6: Cho a,b,c là 3 số thực dương thõa mãn: a2 + 2b2 3c2 . CMR:
Bài 4: Cho đường tròn (O;R) có đường kính BC, lấy điểm A thuộc (O) sao cho AB=R
a. Chứng minh tam giác ABC vuông và tính độ dài BC theo R.
b. Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Trên (O) lấy điểm D sao cho MD=MA (D khác A). Chứng minh MD là tiếp tuyến của (O).
c. Vẽ đường kính AK của (O), MK cắt (O) tại E (E khác K). Gọi H là giao điểm của AD và MO. Chứng minh ME.MK=MH.MO
d. Xác định tâm và bán kính của đường tròn ngoại tiếp tam giác MEH theo R.