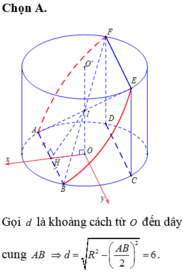
16.Cho đường tròn (O;R), từ điểm A nằm ngoài sao cho OA = 2R kẻ tiếp tuyến AB của (O) (B là tiếp điểm). Từ B kẻ dây BC vuông góc OA, OA cắt (O) tại H.
a. CM: AC là tiếp tuyến của (O);
b. Tính AB theo R và chứng minh ABC là tam giác đều;
c. Từ O kẻ đường thẳng vuông góc với OB cắt AC tại D. CM: DH là tiếp tuyến của (O);
d. Tính AD, DH theo R.



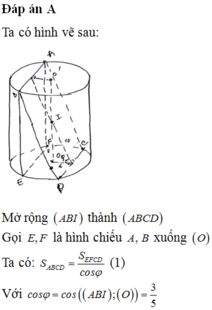

a: Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
Suy ra: \(\widehat{OBA}=\widehat{OCA}\)
hay AC là tiếp tuyến của (O)