Cho hình thoi MNPQ như hình dưới với MN = 8 cm; PQ = 6 cm.
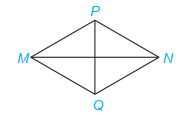
a) Tính diện tích hình thoi MPNQ.
b) Biết MP = 5 cm, tính chu vi hình thoi MPNQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
NV
Nguyễn Việt Dũng
CTVVIP
23 tháng 8 2023
a) Hình bình hành có hai cặp cạnh đối diện song song và bằng nhau
BC = 3 cm
DC = 5 cm
b) Hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
NP = 4 cm
PQ = 4 cm
QM = 4 cm
QT
1
10 tháng 10 2023
Cách 1: - Vẽ đoạn thẳng MN = 4 cm.
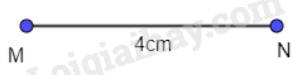
- Lấy M tâm, vẽ đường tròn bán kính 4 cm (hình vẽ).
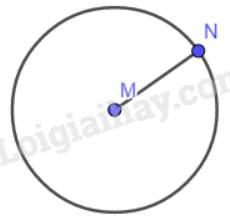
- Trên đường tròn lấy điểm Q, nối M với Q. Khi đó MQ= 4cm.
- Qua N và Q lần lượt vẽ hai đường tròn bán kính bằng 4 cm, hai đường tròn này cắt nhau tại M và P (P khác M).
- Nối P với N và P với Q ta được hình thoi MNPQ. Các cạnh PN=QP =4cm.
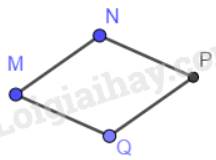
Nhận xét: Hình vẽ có tính chất các cạnh MN=NP=PQ=QM =4cm
Góc \(\widehat {MNQ}\) khác nhau thì sẽ tạo được các hình thoi khác nhau.
Cách 2:
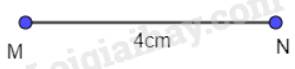
- Vẽ đoạn thẳng MN = 4 cm
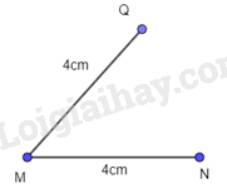
- Vẽ đoạn thẳng MQ = 4 cm
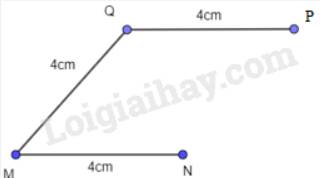
- Từ Q vẽ đường thẳng song song với MN, trên đường thẳng đó lấy điểm P sao cho PQ = 4 cm.
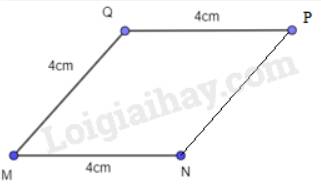
- Nối P với N ta được hình thoi MNPQ.
10 tháng 9 2023
Cạnh QN dài :
\(\left(26+6\right):2=18\left(cm\right)\)
Cạnh MN dài :
\(26-18=8\left(cm\right)\)
Tổng 4 cạnh hình thoi là :
\(8.4=32\left(cm\right)\)
Đáp số...
10 tháng 9 2023
Đính chính
\(QN=\left(26+6\right):2=16\left(cm\right)\)
\(MN=26-16=10\left(cm\right)\)
Bốn cạnh dài :
\(10.4=40\left(cm\right)\)
10 tháng 9 2023
\(MN=\left(26-6\right):2=10\left(cm\right)\)
\(MN\) cũng là cạnh hình thoi, nên tổng 4 cạnh hình thoi là :
\(10.4=40\left(cm\right)\)
10 tháng 8 2018
Diện tích hình thoi ABCD hay diện tích hình bình hành MNPQ là:
18 x 16 : 2 = 144 (cm2)
Chiều cao của hình bình hành MNPQ là:
144 : 9 = 16 (cm)
Đáp số: 16 cm
M
3 tháng 9 2023
a) Để tính diện tích của tam giác AMN, ta sử dụng công thức diện tích tam giác: Diện tích tam giác = 1/2 * cạnh đáy * chiều cao. Với tam giác AMN, cạnh đáy là MN và chiều cao là AH. Vậy diện tích tam giác AMN là: Diện tích AMN = 1/2 * MN * AH.
b) Để tính tổng diện tích của các tam giác AMN, BMQ và CNP, ta cần tính diện tích của từng tam giác và sau đó cộng chúng lại với nhau. Diện tích tam giác BMQ và CNP cũng được tính bằng công thức diện tích tam giác.
Tuy nhiên, để tính chính xác tổng diện tích của các tam giác, ta cần biết giá trị của x và y. Trong trường hợp này, ta biết rằng 2x + y = 23 và y - 2x = 7. Ta có thể giải hệ phương trình này để tìm giá trị của x và y, sau đó sử dụng giá trị đó để tính tổng diện tích của các tam giác.
Tuy nhiên, để tính chính xác tổng diện tích của các tam giác, ta cần biết giá trị của x và y. Trong trường hợp này, ta biết rằng 2x + y = 23 và y - 2x = 7. Ta có thể giải hệ phương trình này để tìm giá trị của x và y, sau đó sử dụng giá trị đó để tính tổng diện tích của các tam giác.
QT
1
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
- Kẻ đoạn MN = 6cm, đo góc MNP bằng \(60^\circ \). Lấy điểm P trên tia còn lại của góc (không chứa điểm M) sao cho NP = 6cm.
Cách 1: - Nối M với P. Lấy O là trung điểm của MP.
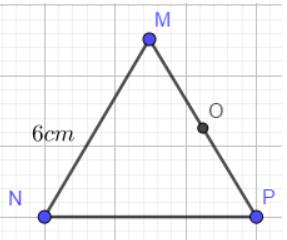
- Kẻ đường thẳng NO, lấy điểm Q sao cho OQ=ON( Q khác N).
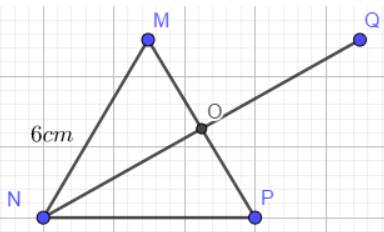
- Nối MQ, QP ta được hình thoi như hình vẽ:
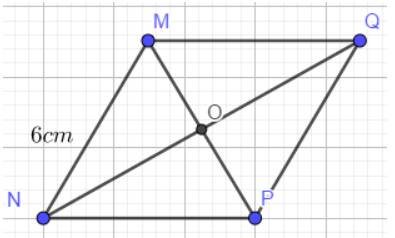
Cách 2:
- Qua M kẻ đường thẳng song song NP, trên đó lấy điểm Q sao cho MQ = 6cm
- Nối PQ
Ta được hình thoi MNPQ cần vẽ
Hic
a) Diện tích hình thoi MPNQ là:
\(S_{MPNQ}=\frac{1}{2}. MN. PQ=\frac{1}{2}. 8.6=24 (cm^2)\)
b) Chu vi hình thoi MPNQ là:
\(C_{MPNQ}=4. MP = 4. 5 = 20 (cm)\)