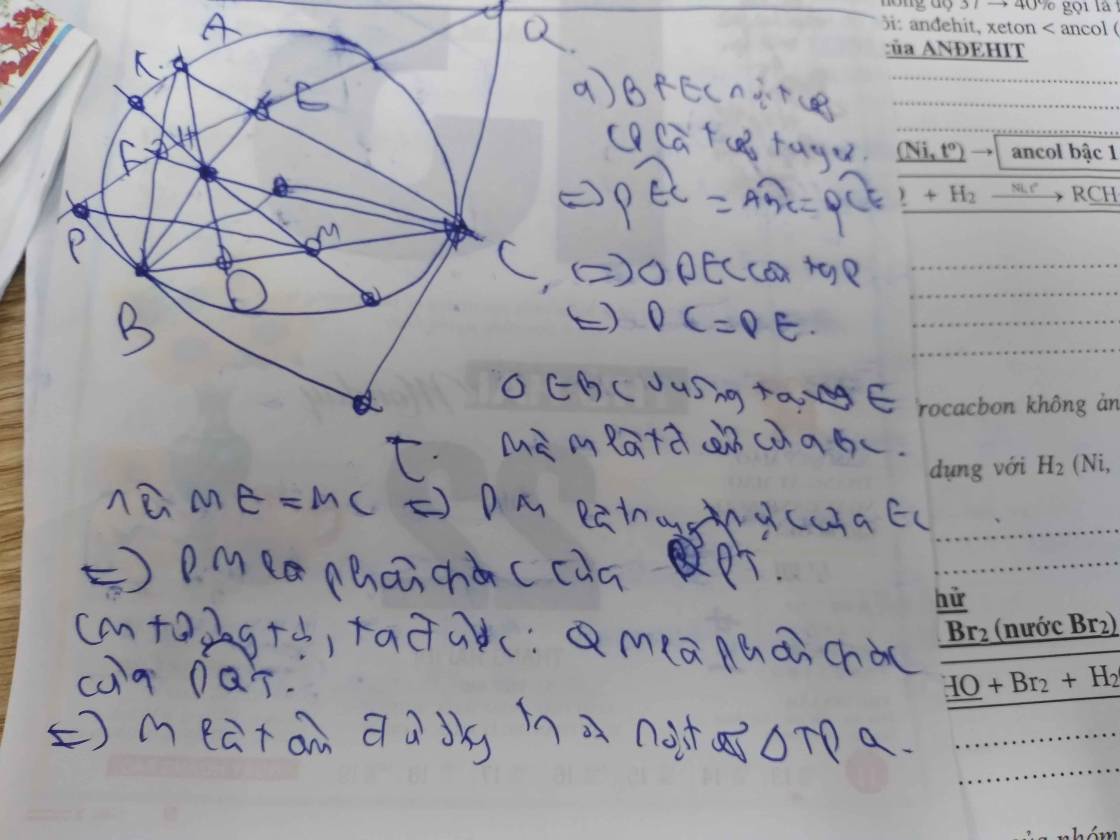
Cho tam giác ABC nội tiếp (O), có đường cao AD, H là trực tâm. (O;OH) cắt AH tại E( khác F). F đối xứng với E qua BC. Gọi N là trung điểm của HE. C/m: AH=2DN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Lời giải:
$\widehat{HBD}=\widehat{EBC}=\widehat{CAD}$ (cùng phụ góc $\widehat{ACB}$)
$\widehat{CAD}=\widehat{CAK}=\widehat{KBC}=\widehat{KBD}$ (góc nt chắn cung $CK$)
$\Rightarrow \widehat{HBD}=\widehat{KBD}$
Xét tam giác vuông tại $D$ là $HBD$ và $KBD$ có:
$\widehat{HBD}=\widehat{KBD}$ (cmt)
$BD$ chung
$\Rightarrow \triangle HBD=\triangle KBD$ (g.c.g)
$\Rightarrow HD=KD$ (đpcm)