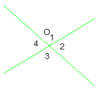
cho hình vẽ . Biết O1=O2 ;O3=O4 và hai tia ox ,On đối nhau . Chỉ ra các tia phân giác trên hình bên ; Tính số đo của góc moy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho hình vẽ. Tính O 1 ^ , O 2 ^ , O 3 ^ , O 4 ^ nếu biết:
a) Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) mà O 1 ^ = 1 2 O 2 ^ nên
1 2 O 2 ^ + O 2 ^ = 180 0 ⇒ 3 2 O 2 ^ = 180 0 ⇒ O 2 ^ = 180 0 .2 3 = 120 0
O 1 ^ = 1 2 O 2 ^ ⇒ O 1 ^ = 1 2 .120 0 = 60 0
Vậy O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = O 4 ^ = 120 0
b) Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) mà O 2 ^ − O 1 ^ = 40 0
⇒ 2 O 2 ^ = 220 0 ⇒ O 2 ^ = 110 0
O 2 ^ − O 1 ^ = 40 0 ⇒ 120 0 − O 1 ^ = 40 0 ⇒ O 1 ^ = 70 0
Vậy O 1 ^ = O 3 ^ = 70 0 ; O 2 ^ = O 4 ^ = 110 0
c) O 1 ^ + O 3 ^ = 130 0 Mà O 1 ^ = O 3 ^ ( Đối đỉnh) nên O 1 ^ = O 3 ^ = 130 0 : 2 = 65 0
O 2 ^ = O 4 ^ = 180 0 − 65 0 = 115 0 ( Hai góc kè bù)
d) O 1 ^ + O 2 ^ + O 3 ^ = 250 0
Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù) nên O 3 ^ = 250 0 − 180 0 = 70 0 .
Do đó O 1 ^ = O 3 ^ = 70 0 ( Đối đỉnh)
O 2 ^ = 180 0 − 70 0 = 110 0 . Suy ra O 4 ^ = O 2 ^ = 110 0 ( Đối đỉnh)
e) O 1 ^ + O 3 ^ = 1 2 ( O 2 ^ + O 4 ^ )
Mà O 1 ^ = O 3 ^ ( Đối đỉnh) , O 4 ^ = O 2 ^ ( Đối đỉnh)
Suy ra 2 O 1 ^ = 1 2 .2 O 2 ^ ⇒ 2 O 1 ^ = O 2 ^
Vì O 1 ^ + O 2 ^ = 180 0 ( Hai góc kề bù). Suy ra O 1 ^ + 2 O 1 ^ = 180 0 ⇒ O 1 ^ = 60 0
O 1 ^ = O 3 ^ = 60 0 ; O 2 ^ = 2 O 1 ^ = 60 0 .2 = 120 0 ⇒ O 4 ^ = O 2 ^ = 120 0

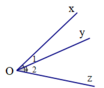
O 1 có đỉnh là O, hai cạnh là Ox và Oy
O 2 có đỉnh là O, hai cạnh là Oy và Oz

bài1
Giả sử trong hình bên, hai đường thẳng xx’ và yy’ cắt nhau tại O, góc xOy bằng 60o
Ta có: ∠xOy = ∠x’Oy'(hai góc đối đỉnh)
Suy ra ∠x’Oy’=60o.
∠xOy + ∠x’Oy’= 180o (hai góc kề bù)
⇒ ∠x’Oy’ = 180o – ∠xOy = 180o – 60o = 120o
∠xOy’ = ∠x’Oy(hai góc đối đỉnh)
⇒∠x’Oy=120o

Ảnh minh họa O x x' y y' 1 2 3 4
a) \(\widehat{O}_1=65^o\)
Có : \(\widehat{O_1}+\widehat{O_2}=180\) (kề bù)
\(=>\widehat{O_2}=180^o-65^o=115^o\)
Mà theo hình vẽ : \(\widehat{O_2}\) đối đỉnh \(\widehat{O}_4\)
Suy ra: \(\widehat{O_4}=\widehat{O_2}=115^o\)(kề bù)
Rồi có : \(\widehat{O_4}+\widehat{O_3}=180^o=>\widehat{O_3}=65^o\)
b) \(O_1=2O_2\)
Và : \(O_1+O_2=180^{^O}=>O_1=180^{^O}-O_2\)
\(=>2O_2=180^{^O}-O_2\)
\(=>3O_2=180^{^O}=>O_2=60^{^O}\)
\(O_1=2O_2=>O_1=2.60^{^O}=120^{^O}\)
c) \(\widehat{O_1}-\widehat{O_2}=20^o\)
\(\Leftrightarrow\widehat{O_1}=20+\widehat{O_2}\)
Và : \(\widehat{O_1}+\widehat{O_2}=180^{^O}\)
Ta có hệ sau : \(\left\{{}\begin{matrix}\widehat{O_1}=20^{^o}+\widehat{O_2}\\\widehat{O_1}+\widehat{O_2}=180^{^O}\end{matrix}\right.\)
\(=>20^{^O}+\widehat{O_2}+\widehat{O_2}=180^{^O}\)
\(=>2\widehat{O_2}=160^{^O}=>\widehat{O_2}=80^{^O}\)
\(\widehat{O_1}-80^{^O}=20^{^O}=>\widehat{O_1}=100^{^O}\)
d) \(O_3+O_1=136^{^O}\)
Mà : \(O_3=O_1\) (đối đỉnh)
\(=>O_3=O_1=\dfrac{136^{^O}}{2}=68^{^O}\)

Ta thấy: o1 và o3 đối đỉnh =>o1=o2
o2 và o4 đối đỉnh =>o2=o4
Tổng 4 góc đối đỉnh là 360 độ.
=> o1+o2+o3+o4=360
=> o1+o2+o1+o2=360
=> 2o1+2o2=360
mà o1=3o2
=> 2.3o2+202=360
=>6o2+2o2=360
=>8o2=360
=>o2=360:8=45(độ)
=>02=04=45 độ
=>o1=o3=3.45=135 độ
Vậy o1=135,o2=45,o3=135,o4=45