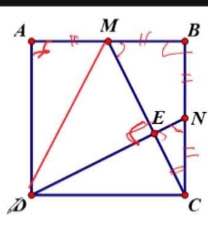
Cho hình vuông ABCD.Gọi M;N lần lượt là trung điểm của AB và BC.Gọi K là giao điểm của CM và DN.Chứng minh AK=AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1
PH
1
HP
9 tháng 11 2015
Gọi K là trung điểm DC, nối AK cắt DI tại O
Chứng mình tam giác DNC = tam giác BMC nên DN vuông góc với CM
Nối AK, AK//CM nên AK cũng vuông góc với DN. tam giác DIC có KO // với CI và K là trung điểm DC nên O là trung điểm DI (đường trung bình tam giác)
Tam giác AID có đường cao AO vừa là trung tuyến nên tam giác AID cân tại A nên AD=AI -> đpcm
21 tháng 11 2023
a: Xét tứ giác AMND có
\(\widehat{MND}=\widehat{ADN}=\widehat{DAM}=90^0\)
=>AMND là hình chữ nhật
b: AMND là hình chữ nhật
=>AM=ND
mà \(AM=\dfrac{AB}{2}\)
nên \(ND=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
nên \(ND=\dfrac{CD}{2}\)
=>N là trung điểm của CD
=>NC=ND
AM=ND
ND=NC
Do đó: AM=NC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của MN
nên O là trung điểm của AC
12 tháng 11 2021
a: Xét tứ giác BMNC có
BM//NC
BM=NC
Do đó: BMNC là hình bình hành
mà \(\widehat{MBC}=90^0\)
nên BMNC là hình chữ nhật
TM
1
ABCDMNKHI
Gọi I là trung điểm của DC. AI giao với DK tại H
+) Tứ giác AMCI là hình bình hành ( AM = CI và AM // CI) => AI // CM
+) Trong tam giác DKC có: HI // CK; I là trung điểm của DC => H là trung điểm của DK (1)
+) Xét tam giác DCN và CBM có: CN = BM ; góc DCN = CBM; DC = BC
=> tam giác DCN = CBM ( c - g - c) => góc CDN = MCB
=> góc CDN + DCM = MCB + DCM = góc DCB = 90o => góc DKC = 90o => DK vuông góc với CM
mà CM // AI => AI vuông góc với DK (2)
Từ (1)(2) => AI là đường trung trực của DK => AD = AK