Cho tam giác ABC, đường cao AH. Gọi M;N là trung điểm của các cạnh AB và AC. Chứng minh:
a) MN là phân giác góc AMH
b) AHM + ABH = 90
( kiến thức lớp 7 )
Giúp mình với mình cần gấp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B1
30 tháng 7 2017
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
AH
Akai Haruma
Giáo viên
2 tháng 5 2023
Lời giải:
Áp dụng định lý Pitago:
$HC=\sqrt{AC^2-AH^2}=\sqrt{4^2-2^2}=2\sqrt{3}$
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH$
$\Rightarrow BH=\frac{AH^2}{CH}=\frac{2^2}{2\sqrt{3}}=\frac{2\sqrt{3}}{3}$
$BC=BH+CH=\frac{2\sqrt{3}}{3}+2\sqrt{3}=\frac{8\sqrt{3}}{3}$
$\Rightarrow MC=BC:2=\frac{4\sqrt{3}}{3}$
$AM$ là trung tuyến ứng với cạnh huyền nên $AM=\frac{BC}{2}=\frac{4\sqrt{3}}{3}$
Chu vi $MAC$:
$MA+MC+AC=\frac{4\sqrt{3}}{3}+\frac{4\sqrt{3}}{3}+4=\frac{12+8\sqrt{3}}{3}$
DD
12 tháng 7 2019
Ban đầu xét tam giác AIB và tam giác AKC có :
góc BAC chung ; góc AKC= góc AIB =90 độ (g)
Do vậy tam giác AIB đồng dạng tam giác AKC (g-g)
=> AI/AB=AK/AC (1)
Xét tam giác AIK và tam giác ABC có :
góc BAC chung ; AI/AB=AK/AC (theo (1))
Do vậy tam giác AIK đồng dạng tam giác ABC (c-g-c)
I
28 tháng 2 2020
xét tam giác AIB và tam giác AKC có :
góc BAC chung ; góc AKC= góc AIB =90 độ (g)
Do vậy tam giác AIB đồng dạng tam giác AKC (g-g)
=> AI/AB=AK/AC (1)
Xét tam giác AIK và tam giác ABC có :
góc BAC chung ; AI/AB=AK/AC (theo (1))
Do vậy tam giác AIK đồng dạng tam giác ABC (c-g-c)
CM
22 tháng 1 2019
Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'
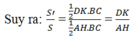
HÌnh bạn tự vẽ nhé:
a) Ta có: Tam giác AHC vuông tại H, N là trung điểm cạnh AC => HN=1/2AC (Trung tuyến ứng với cạnh huyền)
Mà: AN=1/2AC (N là trung điểm AC) => HN=AN
Mặt khác: Tam giác AHB vuông tại H, M là trung điểm cạnh AB => HM=1/2AB (Trung tuyến ứng với cạnh huyền)
Mà: AM=1/2AB (M là trung điểm AC) => HM=AM
Xét tam giác AMN và HMN có:
HN=AN (Chứng minh trên)
HM=AM (Chứng minh trên)
MN chung
=> Tam giác AMN = tam giác HMN (c.c.c)
=>Góc ANM = HNM
=>...
b) Từ: HM=AM (Câu a) => Tam giác AHM cân tại M => Góc AHM=HAB => Góc AHM+ABH=HAB+ABH (1)
Xét tam giác AHB vuông tại H có: Góc HAB+ABH=90 độ (2)
Từ (1) và (2) suy ra: Góc AHM+ABH=90 độ