Cho hình chữ nhật ABCD có AB= 4a, BC= 2a; M là điểm thuộc cạnh CD sao cho CM= \(\dfrac{1}{4}\) CD.
a) CMR AC ⊥ BM
b) Tính tanMAC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

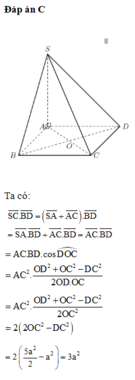
Đáp án C
Ta có: S C → . B D → = S A → + A C → . B D → = S A → . B D → + A C → . B D → = A C → . B D →
= A C . B D . cos D O C ^ = A C 2 . O D 2 + O C 2 − D C 2 2 O D . O C
= A C 2 . O D 2 + O C 2 − D C 2 2 O C 2 = 2 2 O C 2 − D C 2
= 2 5 a 2 2 − a 2 = 3 a 2
Do đó: cos S C → , B D → = S C → . B D → S C . B D = 3 a 2 3 a . a 5 = 1 5
Vậy cos S C , B D = cos S C → , B D → = 1 5


Khi quay hình chữ nhật ABCD quanh đường AB thì được hình trụ có
R=BC=a, h=AB=2a
\(S_{XQ}=2\cdot pi\cdot a\cdot2a=4\cdot pi\cdot a^2\)

Lời giải:
Quay hcn $ABCD$ xung quanh trục $\Delta$ là trung trực của $BC$ là được khối trụ có bán kính đáy là $R=BC:2 =a$ và chiều cao là $AB=3a$
Thể tích khối trụ là:
$V=S_{đáy}.h = \pi R^2h = \pi .a^2.3a=3a^3\pi$

Lời giải:
Kẻ tia $AL$ đối tia $AB$ sao cho $AB=AL$. Từ $L$ kẻ $LK\perp DC$
\(|\overrightarrow{AB}+\overrightarrow{AC}|=|\overrightarrow{LA}+\overrightarrow{AC}|=|\overrightarrow{LC}|\)
\(=LC=\sqrt{LK^2+KC^2}=\sqrt{BC^2+BL^2}=\sqrt{BC^2+(2AB)^2}=\sqrt{(4a)^2+(2.2a)^2}=4\sqrt{2}a\)

Bài này bạn đã đăng tại đây:
https://hoc24.vn/cau-hoi/cho-hinh-chu-nhat-abcd-co-do-dai-canh-ab2a-bc4atinh-do-dai-vecto-abvecto-ac.2659817639735

\(\left|\overrightarrow{AB}-\overrightarrow{BC}\right|=\left|\overrightarrow{AB}+\overrightarrow{CB}\right|=BD=a\sqrt{6}\)

Đáp án B
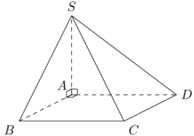
Diện tích đáy ABCD là SABCD = AB. BC = a.2a = 2a2.
Thể tích khối chóp S.ABCD là:
V = 1 3 . S A . S A B C D = 1 3 . 2 a . 2 a 2 = 4 a 3 3


a: Xét ΔBAC vuông tại B và ΔCBM vuông tại C có
BA/BC=BC/CM
=>ΔBAC đồng dạng với ΔCBM
=>góc BAC=góc CBM
=>góc CBM+góc ACB=90 độ
=>BM vuông góc AC
b: AM=căn AD^2+DM^2=a*căn 13
AC=căn AB^2+BC^2=a*2*căn 5
MC=a
\(cosMAC=\dfrac{AM^2+AC^2-MC^2}{2\cdot AM\cdot AC}=\dfrac{8}{\sqrt{65}}\)
\(1+tan^2MAC=\dfrac{1}{cos^2MAC}\)
=>\(tan^2MAC+1:\dfrac{64}{65}-1=\dfrac{1}{64}\)
=> tan MAC=1/8