cho hình bình hành ABCD ,gọi I là giao điểm của AC và BD ;M,N theo thứ tự là trung điểm của ID,IB
a/ chứng minh AM//CN
b/kéo dài AM cắt DC tại E.Chứng minh DE =1/2 EC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 9 2018
* Ta có ABCD là hình bình hành nên AB = CD; ABCD đồng thời là hình thang có 2 đáy là AB và CD.
Vì E và F lần lượt là trung điểm của AD và BC nên EF là đường trung bình của hình thang ABCD
Suy ra: EF// AB// CD và
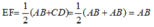
(vì AB = CD)
* Xét tứ giác ABFE có AB// EF và AE// BF nên ABFE là hình bình hành
Tương tự, tứ giác EFCD là hình bình hành.
* Theo tính chất hình bình hành ta có: I là trung điểm của AC và BD.
Tam giác ACD có E và I lần lượt là trung điểm của AD và AC nên EI là đường trung bình của tam giác
Chọn đáp án C
15 tháng 8 2017
Vì tứ giác ABCD là hình bình hành nên:
- AB = CD => AM = CN
- AB // CD => AM //CN
Tứ giác AMCN có cặp cạnh AM, CN song song và bằng nhau nên nó là hình bình hành.
b) chứng minh M, O, N thẳng hàng
* AC và BD là hai đường chéo của hình bình hành ABCD nên chúng cắt nhau tại trung điểm của mỗi đường.
Do đó, O là trung điểm AC
* AC và MN là hai đường chéo của hình bình hành AMCN nên MN phải đi qua trung điểm O của AC
hay M, O, N thẳng hàng.
chuk hoc gioi
13 tháng 11 2021
Xét ΔBDC có
F là trung điểm của BC
I là trung điểm của BD
Do đó: FI là đường trung bình của ΔBDC
Suy ra: FI//DC và FI=DC/2(1)
Xét ΔADC có
E là trung điểm của AD
I là trung điểm của AC
Do đó: EI là đường trung bình của ΔADC
Suy ra: EI//DC và EI=DC/2(2)
Từ (1) và (2) suy ra E và F đối xứng với nhau qua I
3 tháng 9 2021
a: Xét tứ giác BMDN có
BM//ND
BM=ND
Do đó: BMDN là hình bình hành
Suy ra: MD//BN