Bài 3: Cho ∆ ABC vuông tại A, đường cao AH biết HB=4cm ; HC= 9cm . a) Tính AB và AH. b) Từ HE vuông góc với AB, HF vuông góc với AC Tử giác AEHF là hình gì? Tính EF ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BV
2
AH
Akai Haruma
Giáo viên
4 tháng 11 2023
Lời giải:
a.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=3.4=12$
$\Rightarrow AH=\sqrt{12}=2\sqrt{3}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=3(3+4)=21$
$\Rightarrow AB=\sqrt{21}$ (cm)
15 tháng 10 2017
bạn vẽ hình nha mk ko biết vẽ sorry
Áp dung định lí pytago vào tam giác ABC vuông tại A đường cao AH ta có:
\(AB^2+AC^2=BC^2\)
hay \(4^2+3^2=BC^2\)
\(\Rightarrow BC^2=16+9\)
\(\Rightarrow BC^2=25\)
\(\Rightarrow BC=5\left(cm\right)\)
Áp dụng hệ thức giữa cạnh và đường vào tam giác vuông \(ABC\)vuông tại \(A\) đường cao \(AH\) ta có:
+ \(AB^2=BH.BC\)
hay \(4^2=HB.5\)
\(\Rightarrow HB=16:5\)
\(\Rightarrow HB=3,2\left(cm\right)\)
+ \(AC^2=HC.BC\)
hay \(3^2=HC.5\)
\(\Rightarrow HC=9:5\)
\(\Rightarrow HC=1,8\left(cm\right)\)
vậy \(HB=3,2cm\)
\(HC=1,8cm\)
TA
1
28 tháng 6 2023
TK:
Ta có tam giác vuông ABC với đường cao AH.
Theo định nghĩa, đường cao AH là đoạn thẳng vuông góc với cạnh đối diện và đi qua đỉnh của tam giác.
Vì tam giác ABC vuông tại A, nên AH là đường cao của tam giác.
Áp dụng định lý Pythagoras trong tam giác vuông ABC, ta có:
\(AB^2+AC^2=BC^2\)
\(4^2+7,5^2=BC^2\)
\(16+56,25=BC^2\)
\(72,25=BC^2\)
\(BC\approx8,5cm\)
Vì AH là đường cao của tam giác ABC, nên AH chia BC thành hai đoạn HB và HC.
\(HB=BC\times\left(\dfrac{AB}{AC}\right)\)
\(HB=8,5\times\left(\dfrac{4}{7,5}\right)\)
\(HB\approx4,53cm\)
\(HC=BC-HB\)
\(HC=8,5-4,53\)
\(HC\approx3,97cm\)
Vậy \(HB\approx4,53cm\) và \(HC\approx3,97cm\)
CM
11 tháng 2 2018
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
+) Áp dụng hệ thức về cạnh và đường cao trng tam giác vuông ABC với AH là đường cao ta có:
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
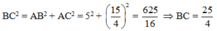
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có:
+) Diện tích tam giác ABC với AH là đường cao ta có:
Vậy AB = 5cm, AC = 15 4 cm; AM = 25 8 cm; S ∆ A B C = 75 8 c m 2 .
Đáp án cần chọn là: A
15 tháng 5 2022
\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)
BC=HB+HC=6,25(cm)
AM=BC/2=3,125(cm)
\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)
\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)
15 tháng 5 2022
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :
\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)
+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\)
\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\)
\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)
+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :
\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)
\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)
+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :
\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Lời giải:
Áp dụng định lý Pitago cho tam giác vuông $ABH$:
$BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-4^2}=3$ (cm)
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH\Rightarrow CH=\frac{AH^2}{BH}=\frac{4^2}{3}=\frac{16}{3}$ (cm)
$BC=BH+CH=3+\frac{16}{3}=\frac{25}{3}$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{4^2+(\frac{16}{3})^2}=\frac{20}{3}$ (cm)
16 tháng 9 2021
Áp dụng HTL tam giác:
\(\left\{{}\begin{matrix}AH^2=BH\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}HC=\dfrac{AH^2}{BH}=\dfrac{16}{3}\left(cm\right)\\AB^2=3\left(3+\dfrac{16}{3}\right)=25\left(cm\right)\\AC^2=\dfrac{16}{3}\left(3+\dfrac{16}{3}\right)=\dfrac{400}{9}\left(cm\right)\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}HC=\dfrac{16}{3}\left(cm\right)\\AB=5\left(cm\right)\\AC=\dfrac{20}{3}\left(cm\right)\end{matrix}\right.\)
\(BC=\sqrt{AB^2+AC^2}=\dfrac{25}{3}\left(cm\right)\left(pytago\right)\)
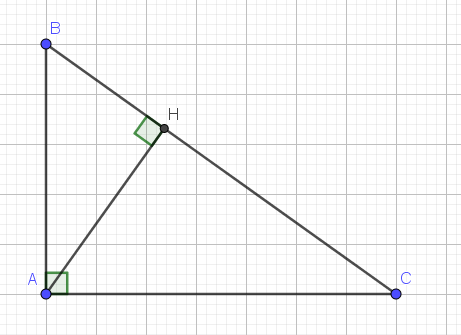
a)áp dụng hệ thức lượng về cạnh và đường cao trong tg vuông
=>AH2=HB.HC
=>AH=√4.9=6cm
vì HB+HC=BC
=>BC=9+4=13cm
áp dụng hệ thức lượng về cạnh và đường cao trong tg vuông
=>AB2=BH.BC
=>AB=√4.13=2√13cm
b)xét tứ giác AEHF
AEH=EAF=AFH=90
=>AEHF hình chữ nhật
=>EF=AH=6cm