Cho hình bình hành ABCD, trên AB;BC;CD;DA lấy các điểm E;F;G;H sao cho EG không song song với AD và SEFGH = 1/2 SABCD. Chứng minh rằng FH//CD?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 7 2023
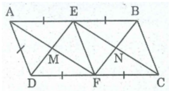
a: Xét tứ giác AMCN có
AM//NC
AM=CN
=>AMCN là hình bình hành
b:
AM+MB=AB
CN+ND=CD
mà AM=CN và AB=CD
nên MB=ND
Xét tứ giác DMBN có
BM//DN
BM=DN
=>DMBN là hình bình hành
CM
28 tháng 4 2017
Ta có: Hình chữ nhật EMFN là hình thoi ⇒ ME = MF
ME = 1/2 DE (tính chất hình thoi)
MF = 1/2 AF (tính chất hình thoi)
Suy ra: DE = AF
⇒ Tứ giác AEFD là hình vuông (vì hình thoi có 2 đường chéo bằng nhau)
⇒ ∠ A = 90 0 ⇒ Hình bình hành ABCD là hình chữ nhật.
Ngược lại: ABCD là hình chữ nhật ⇒ ∠ A = 90 0
Hình thoi AEFD có ∠ A = 90 0 nên AEFD là hình vuông
⇒ AF = DE ⇒ ME = MF (tính chất hình vuông)
Hình chữ nhật EMFN là hình vuông (vì có 2 cạnh kề bằng nhau)
Vậy hình chữ nhật EMFN là hình vuông nếu ABCD là hình chữ nhật có AB = 2AD.
.
19 tháng 8 2021
a: Ta có: AE+EB=AB
DF+FC=DC
mà AE=FC
và AB=DC
nên EB=DF
Xét tứ giác EBFD có
EB//DF
EB=DF
Do đó: EBFD là hình bình hành
Suy ra: DE=BF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
4 tháng 8 2016
- EACF: có AF = CF và AF song song CF ( do AD song song CF) nên EACF là hình bình hành
- DMBN tương tự nhá
22 tháng 7 2023
Xét ΔMBN và ΔPDQ có
MB=PD
góc B=góc D
BN=DQ
=>ΔMBN=ΔPDQ
=>MN=PQ
Xét ΔAMQ và ΔCPN có
AM=CP
góc A=góc C
AQ=CN
=>ΔAMQ=ΔCPN
=>MQ=PN
mà MN=PQ
nên MNPQ là hình bình hành