Cho hình vuông ABCD, \(E\in AB;F\in AD\) sao cho AE=DF. Gọi M, N lần lượt là trung điểm của EF, CE. Chứng minh \(MN\perp DE\) và \(MN=\dfrac{1}{2}DE\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


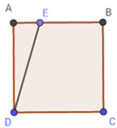
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 102 = 100 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 10 ) .10 2 = 5 (x+10)
Vì diện tích hình thang vuông BCDE bằng 4 5 diện tích hình vuông ABCD nên ta có:
SBCDE = SABCD = 5(x + 10) = 4 5 .100 óx + 10 = 16 ó x = 6 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 6 m.
Đáp án cần chọn là: B

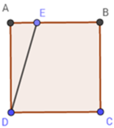
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 20 ) .20 2 = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng 3 4 diện tích hình vuông ABCD nên ta có:
SBCDE = 3 4 SABCD = 10(x + 20) = 3 4 .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D

CM: EFGH là hình vuông (bạn tự chứng minh nhé)
HD = EA = BF = CG = x
Ta có: AH = AD - HD = 4 - x (cm)
Áp dụng định lí Py-ta-go vào \(\Delta AHE\)
=> HE2 = AE2 + AH2
Diện tích hình vuông EFGH:
HE2 = x2 + ( 4 - x)2
= x2 + 16 - 8x + x2
= 2x2 + 16 - 8x
= 2.(x2 - 4x + 8)
= 2.[(x - 2)2 + 4]
= 2.(x - 2)2 + 8
Vì 2.(x - 2)2 \(\ge\)0
=> 2.(x - 2)2 + 8 \(\ge\)8
Dấu '=' xảy ra khi:
x - 2 = 0 => x = 2 (cm)
Vậy HD = 2cm thì hình vuông EFGH có diện tích nhỏ nhất là 8 cm2
Chúc bạn học tốt!!!
