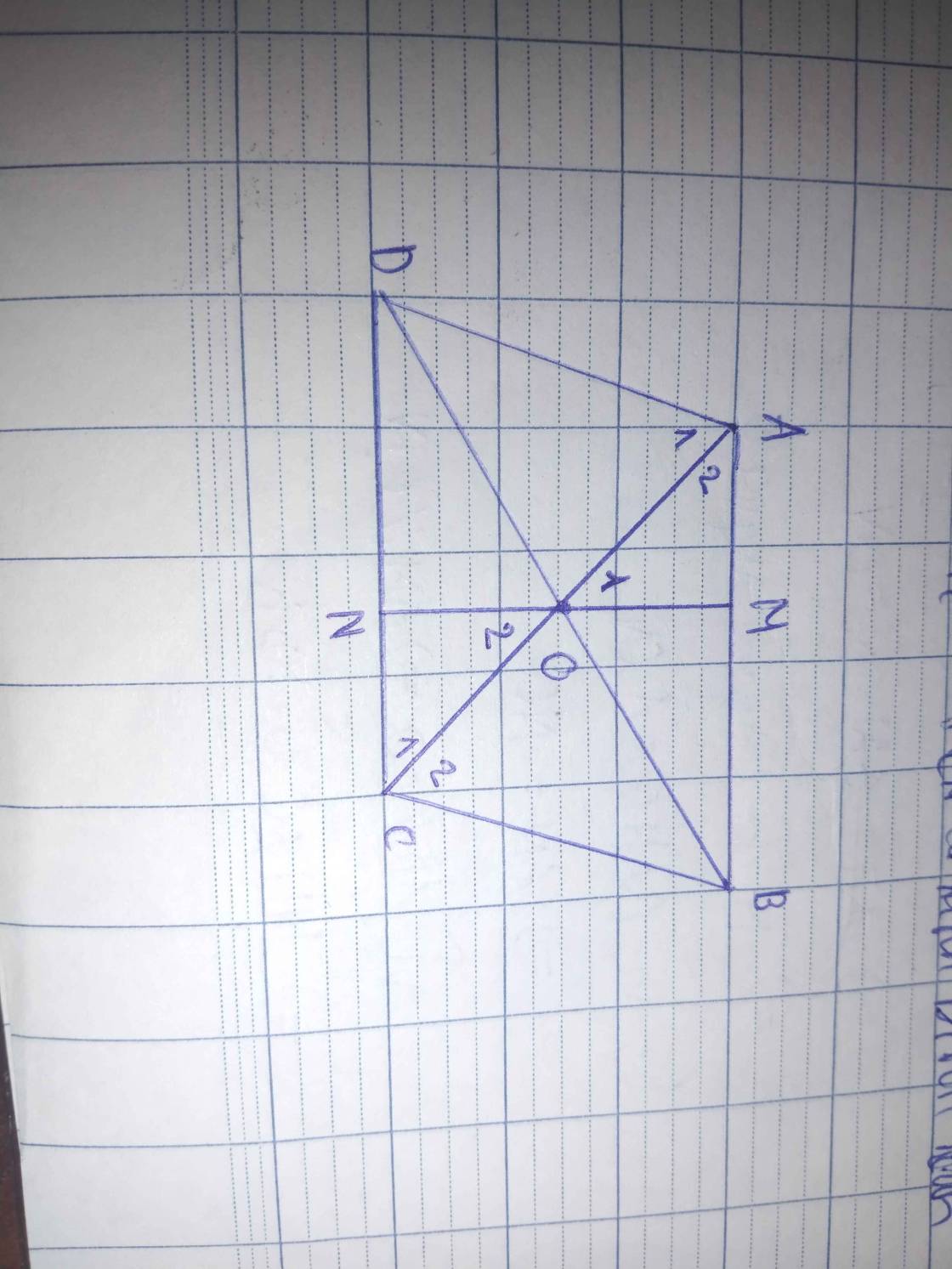
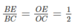B1: cho hình bình hành ABCD có M là trung điểm của AB và N là trung điểm của CD.
1) C/m : tứ giác AMND là hình bình hành.
2) C/m: tứ giác AMCN là hình bình hành.
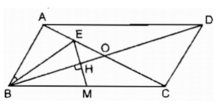
B2: Cho hình bình hành ABCD. Gọi O là giao điểm của 2 đường chéo AC và BD. Một đường thẳng qua O cắt AB tại E và cắt CD tại F.
1) C/m: O là trung điểm của EF.
2) C/m: tứ giác AECF là hình bình hành
3) C/m: tứ giác BDEF là hình bình hành.
B3: cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE=CF. Gọi O là giao điểm của AC và BD.
1) C/m: tứ giác AECF là hình bình hành.
2) C/m: O là trung điểm của EF.
B4: Cho hình bình hành ABCD có hai đường chéo AB và CD cắt nhau tại O. Gọi M,N,P,Q lần lượt là tủng điểm của các đoạn OA, OB, OC, OD.
1)C/m : tứ giác MNPQ là hình bình hành.
2) C/m: các tứ giác ANCQ , BPDM là các hình bình hành.
Giúp mik với nha, thanks !!!!