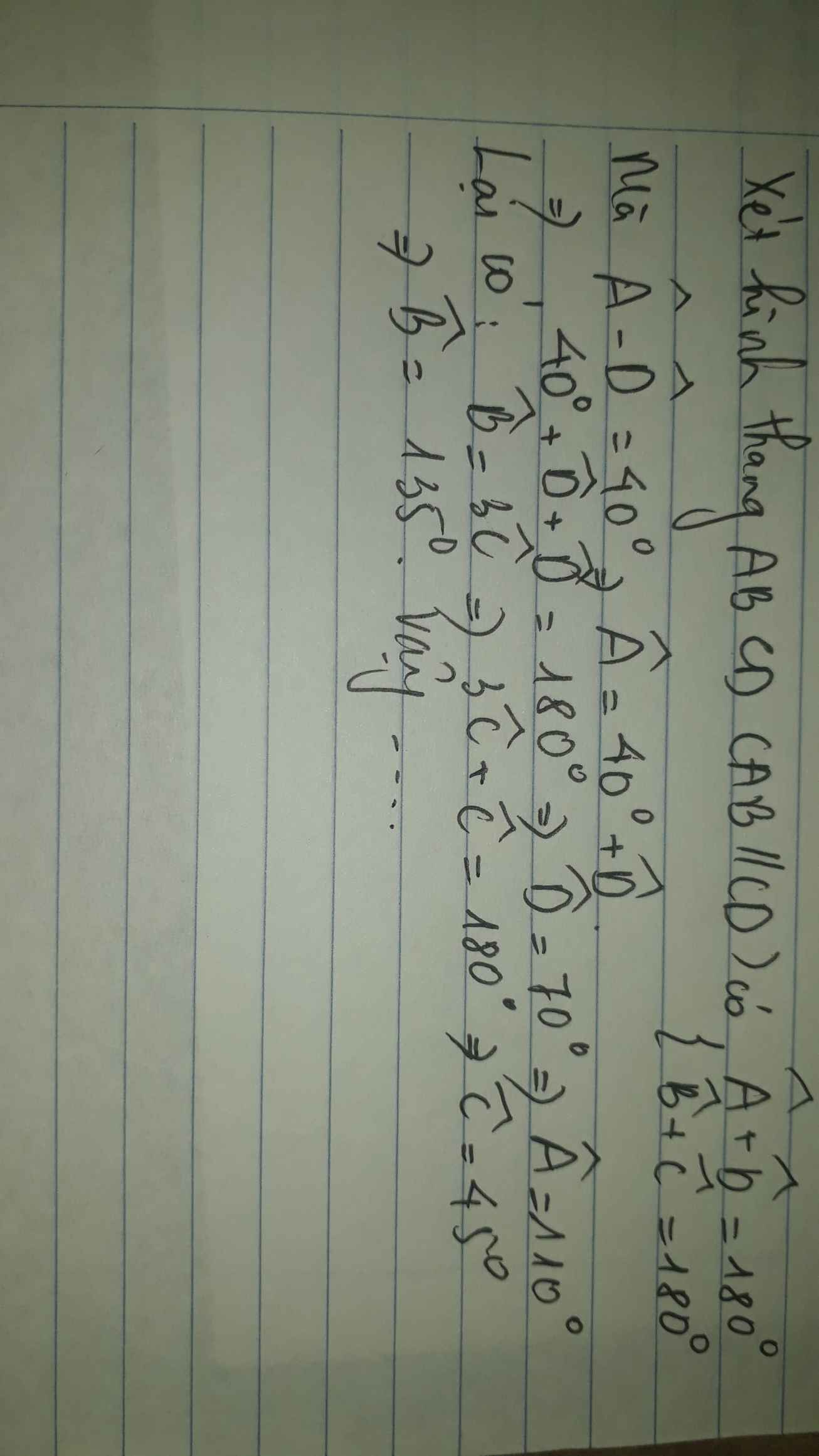Hình thang ABCD (AB // CD) có B-C=60; D=4/5.A. Tính các góc của hình thang ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 8 2021
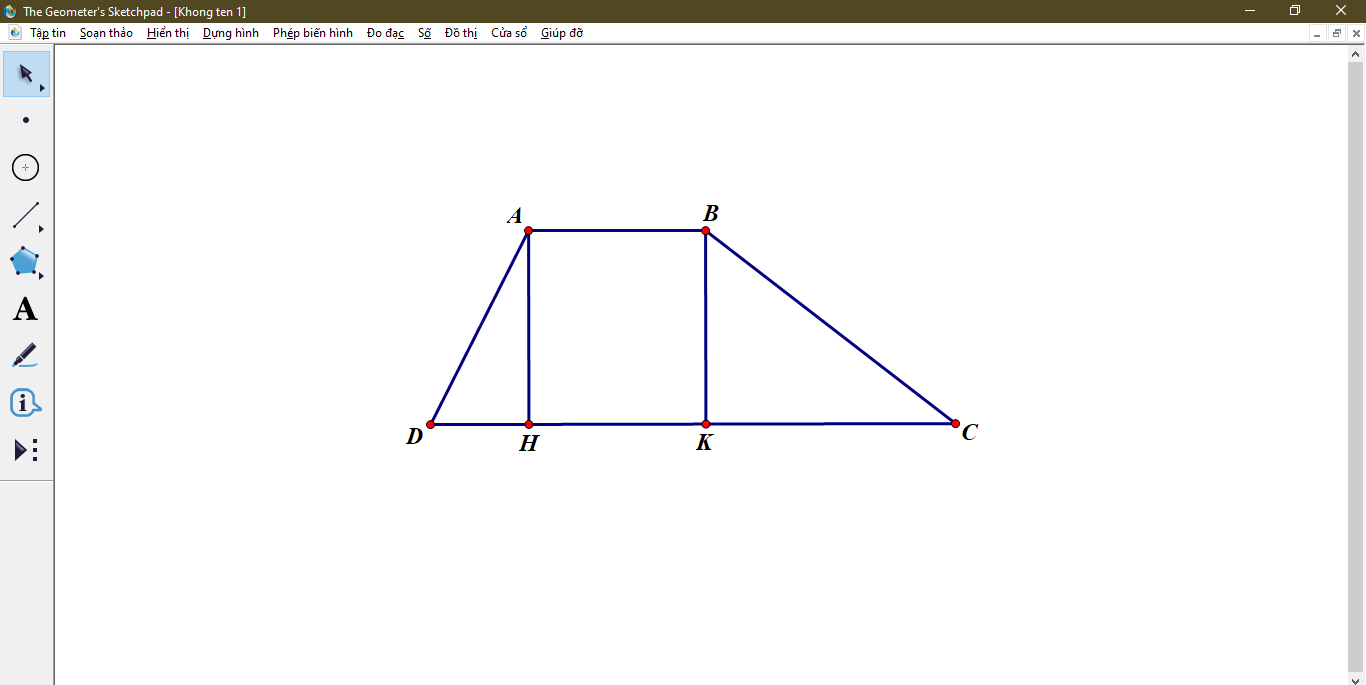
Kẻ đường cao AH và đường cao BK . ⇒AB=HK=1cm
Nên ta có : DH+CK=4 (1)
Theo tỉ số lượng giác cho tam giác ADH và BCK ta lại có :
\(\left\{{}\begin{matrix}AH=tan60\cdot DH\\BK=tan30\cdot CK\end{matrix}\right.\)\(\Rightarrow tan60\cdot DH=tan30\cdot CK\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình :
\(\left\{{}\begin{matrix}DK+CK=4\\\sqrt{3}DH-\dfrac{\sqrt{3}}{3}CK=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}DH=1\\CK=3\end{matrix}\right.\)
\(\Rightarrow AH=tan60\cdot DH=\sqrt{3}\cdot1=\sqrt{3}\left(cm\right)\)
\(\Rightarrow S_{ABCD}=12\cdot AH\cdot\left(AB+CD\right)=12\cdot\sqrt{3}\cdot\left(1+5\right)=3\sqrt{3}\left(cm^2\right)\)
Tick hộ nha bạn 😘
1 tháng 8 2016
Hinh thang ABCD ( AB // CD ) nên góc B + góc C = 180 độ (1) ( hai góc trong cùng phái bù nhau )
ta lại có : góc B - góc C = 60 độ ( 2).
Cộng vế với vế (1) và (2) ta được : 2B = 240 độ => B = 120 độ => C = 60 độ
tương tự: Góc A + góc D = 180 (3) độ .
mà góc D = 4/5 góc A . thế vào (3) ta được: 9/5A = 180 độ => A = 100 độ => D = 80 độ
27 tháng 8 2023
ABCD là hình thang cân
=>góc ADC=góc DCB=180-60=120 độ
AB//CD
=>góc KCB=góc CBA=60 độ
Xét tứ giác ABKH có
KH//AB
AH//BK
Do đó: ABKH là hình bình hành
=>AB=KH=8cm
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc ADH=góc BCK
Do đó: ΔAHD=ΔBKC
=>HD=KC=2cm
HD+DC+CK=HK
=>2+2+DC=8
=>DC=4(cm)
23 tháng 9 2017
A B C D O
Gọi O là trung điểm của CD.
Hình thang ABCD có ^C=^D=600 => ABCD là hình thang cân => AD=BC.
Mà CD=2AD => CD=2BC.
Do O là trung điểm CD => AD=OD=OC=BC (1)
Xét tam giác AOD: ^D=600; AD=OD => Tam giác AOD đều => AD=DO=AO (2)
Tương tự: Tam giác BOC đều => BC=OC=BO (3)
Từ (1); (2) và (3) => OA=OB=OC=OD => 4 điểm A,B,C,D cùng nằm trên đường tròn tâm O (đpcm)