1)cho góc vuông xOy .một đường tròn tiếp xúc với Ox TẠI A và cắt tia OY TẠI 2 ĐIỂM B;C. biết OA=2cm. tính \(\frac{1}{AB^2}+\frac{1}{AC^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cái chỗ có chữ suy ra cũng cần phải chứng minh đó bạn chứ không suy ra thẳng đâu,nhiều khi hắn còn khó hơn vế trước á
Vì OA là tiếp tuyến \(\Rightarrow\angle OAE=\angle OCA\) (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
Xét \(\Delta OAE\) và \(\Delta OCA:\) Ta có: \(\left\{{}\begin{matrix}\angle OAE=\angle OCA\\\angle AOCchung\end{matrix}\right.\)
\(\Rightarrow\Delta OAE\sim\Delta OCA\left(g-g\right)\Rightarrow\dfrac{OA}{OC}=\dfrac{OE}{OA}\Rightarrow OA^2=OC.OE\)
\(\Delta OAE\sim\Delta OCA\Rightarrow\dfrac{AE}{AC}=\dfrac{OA}{OC}\)
Tương tự \(\Rightarrow\Delta OBE\sim\Delta OCB\left(g-g\right)\Rightarrow\dfrac{BE}{BC}=\dfrac{OB}{OC}\)
mà \(OB=OA\) (tính chất tiếp tuyến) \(\Rightarrow\dfrac{BE}{BC}=\dfrac{AE}{AC}\Rightarrow AC.BE=AE.BC\)


a,Chứng minh tam giác MPE đồng dạng với tam giác KPQ.
+PK là phân giác góc QPO.
=>^MPE = ^KPQ.(α) .
+ Tam giác OMN đều .=>^EMP=120 độ.
+ QK cũng là phân giác ^OQP.
=>^QKP = 180 - (^KQP+^KPQ).
Mà 2^KQP + 2^KPQ =180- 60 =120 độ.
=>^QKP=120 độ. Do đó:^EMP = ^QKP. (ß) .
Từ (α) và (ß), ta có tam giác MPE đồng dạng với tam giác KPQ.
b, Chứng minh tứ giác PQEF nội tiếp được trong đường tròn.
Do hai tam giác MPE và KPQ đồng dạng nên:^MEP=^KQP , hay: ^FEP=^FQP.
Suy ra, tứ giác PQEF nội tiếp được trong đường tròn.
c, Gọi D là trung điểm của đoạn PQ. Chứng minh tam giác DEF là một tam giác đều.
Do hai tam giác MPE và KPQ đồng dạng nên: PM/PK =PE/PQ . Suy ra: PM/PE =PK/PQ .
Ngoài ra: ^MPK=^EPQ . Do đó, hai tam giác MPK và EPQ đồng dạng.
Từ đó:^PEQ=^PMK=90độ .
Suy ra, D là tâm của đường tròn ngoại tiếp tứ giác PQEF.
Vì vậy, tam giác DEF cân tại D.
Ta có: ^FDP=2^FQD=^OQP ; ^EDQ=2^EPD=^OPQ .
^FDE=180 - (^FDP+^EDQ) =^POQ =60độ.
Từ đó, tam giác DEF là tam giác đều.


a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C

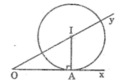
* Phân tích
Giả sử đường tròn tâm I dựng được thỏa mãn điều kiện bài toán.
- Đường tròn tâm I tiếp xúc với Ox tại A nên I nằm trên đường thẳng vuông góc với Ox kẻ từ A
- Tâm I nằm trên tia Oy nên I là giao điểm của Oy và đường thẳng vuông góc với Ox tại A
* Cách dựng
- Dựng đường vuông góc với Ox tại A cắt Oy tại I
- Dựng đường tròn (I; IA)
* Chứng minh
Ta có: I thuộc Oy; OA ⊥ IA tại A
Suy ra Ox là tiếp tuyến của đường tròn (I; IA) hay (I; IA) tiếp xúc với Ox.
* Biện luận
Vì góc (xOy) là góc nhọn nên đường thẳng vuông góc với Ox tại A luôn cắt tia Oy nên tâm I luôn xác định và duy nhất.

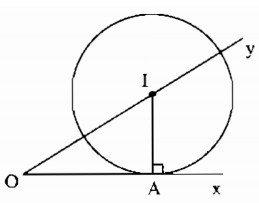
* Phân tích
Giả sử đường tròn tâm I dựng được thỏa mãn điều kiện bài toán.
− Đường tròn tâm I tiếp xúc với Ox tại A nên I nằm trên đường thẳng vuông góc với Ox kẻ từ A.
− Tâm I nằm trên tia Oy nên I là giao điểm của Oy và đường thẳng vuông góc với Ox tại A.
* Cách dựng
− Dựng đường vuông góc với Ox tại A cắt Oy tại I.
− Dựng đường tròn (I; IA).
* Chứng minh
Ta có: I thuộc Oy, OA ⊥ IA tại A.
Suy ra Ox là tiếp tuyến của đường tròn ( I;IA)
hay (I; IA) tiếp xúc với Ox.
* Biện luận
Vì góc xOy là góc nhọn nên đường thẳng vuông góc với Ox tại A luôn cắt tia Oy nên tâm I luôn xác định và duy nhất.