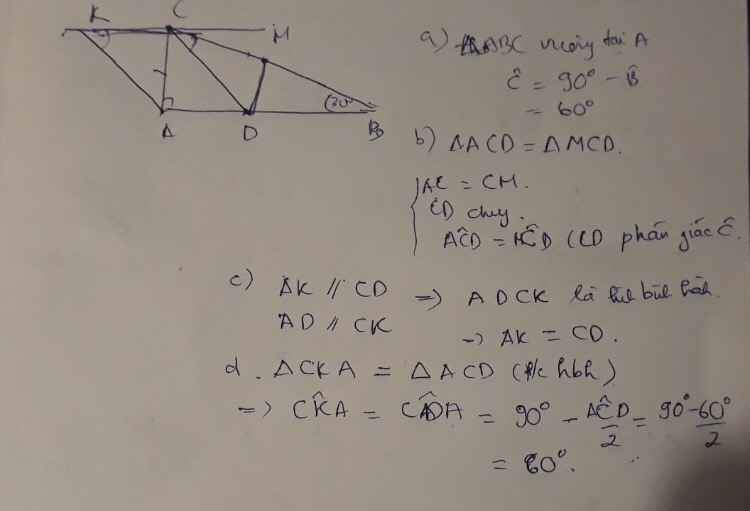
CHO TAM GIÁC ABC VUÔNG TẠI A CÓ GÓC B =30 ĐỘ.QUA C VẼ ĐƯỜNG THẲNG XY VUÔNG GÓC VỚI CA .TỪ A KẺ ĐƯỜNG THẲNG SONG SONG VỚI CD CẮT XY Ở K ; CHỨNG MINH AK = CD ;TÍNH GÓC AKC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
22 tháng 8 2019
a, Xét ∆ABC vuông tại A có: B + C = 90o
=> 30o + C = 90o
=> C = 60o
b, Vì CD là tia phân giác của C
=> ACD = DCB = ACB/2 = 60o/2 = 30o
Xét ∆ACB và ∆MCD
Có: AD: cạnh chung (gt)
ACD = DCM (vì CD là tia p/g của C)
CA = CM (gt)
=> ∆ACB = ∆MCD (c.g.c)
c, XY vuông góc CA => KCA = 90o
Vì AK // CD => CKA = CDA (2 góc so le trong)
Xét ∆CAK vuông tại C và ∆ADC vuông tại A
Có: CA: cạnh chung
CKA = CDA (cmt)
=> ∆CAK = ∆ADC (cgv-gn)
=> AK = DC (2 cạnh tương ứng)
d, Vì ∆CAK = ∆ADC (câu c)
=> KAC = ACD (2 góc tương ứng)
Mà ACD = 30o
=> KAC = 30o
Xét ∆KAC vuông tại C có: KAC + AKC = 90o
=> 30o + AKC = 90o
=> AKC = 60o
11 tháng 7 2017
mình vẽ hình rồi, còn phần chứng minh làm như bạn Trần Hoàng Việt nha!!
11 tháng 7 2017
a) Ta có : A=900 ; B=300
=> C=180-A-B=180-90-30=60
b) Xét tam giác ACD và MCD ta có :
CD chung (1)
CM=CA (gt)(2)
góc ACD=góc DCM (gt) (3)
Từ (1)(2)(3) =>\(\Delta\)ACD=\(\Delta\)MCD (c.g.c)
c) Ta có :AK//CD; CK//AD => tứ giác ADCK là hình bình hành
=>AK=CD (cặp cạnh tương ứng )
d)Ta có : \(\widehat{BDC}\)=180-30-60:2=1200
\(\widehat{CPA}\)=180-120=60
Do ADCK là hình bình hành nên \(\widehat{CPA}\)=\(\widehat{AKC}\)=\(60^0\)
21 tháng 5 2018
hình tự vẽ bn nha a) ta có:tam giác abc vuông tại a => bac = 90 xét tam giác abc có: abc + acb + cab = 180(t/c) mà bac = 90(cmt) ; acb = 36(gt) => 90 +36 + abc = 180 126 + abc = 180 abc= 54
b) ta có: abd = ebd ( vì bd là phân giác của abc) xét tam giác abd và tam giác ebd có: ba=be(gt) ; abd=ebd(cmt) : chung cạnh bd => tam giác abd = tam giác ebd ( c.g.c) (đpcm)
c) ta có: xy vuông góc với ab(gt) => tam giác abk vuông tại b tam giác abc vuông tại a(gt) => ab vuông góc với ac ta có: xy vuông góc với ab (gt) ab vuông góc với ac(cmt) => xy song song với ac(t/c) => bak = abd ( so le trong) xét tam giác abk vuông tại b và tam giác bad vuông tại a có: bak=abd(cmt) ; chung cạnh ba => tam giác abk= tam giác abd ( cgv-gnk) => ak=bd(2 cạnh tương ứng)
9 tháng 12 2016
Kí hiệu tam giác là t/g nhé
a) t/g ABC vuông tại A có: ACB + ABC = 90o
=> 36o + ABC = 90o
=> ABC = 90o - 36o = 54o
b) Xét t/g ABD và t/g EBD có:
AB = BE (gt)
ABD = EBD ( vì BD là phân giác của ABE)
BD là cạnh chung
Do đó, t/g ABD = t/g EBD (c.g.c) (đpcm)
c) Xét t/g ABD vuông tại A và t/g BAK vuông tại B có:
ABD = BAK (so le trong)
AB là cạnh chung
Do đó, t/g ABD = t/g BAK ( cạnh góc vuông và góc nhọn kề)
=> BD = AK (2 cạnh tương ứng) (đpcm)
d) Dễ thấy, CA, BH, FE là 3 đường cao của t/g BCF
Do đó 3 đường này cùng đi qua 1 điểm
Mà BH và CA cắt nhau tại D
Nên EF đi qua D
=> E, D, F thẳng hàng (đpcm)
9 tháng 12 2016
Câu d sai, lm lại
Nối đoạn FD
t/g BAC = t/g BEF ( cạnh góc vuông và góc nhọn kề)
=> BC = BF (2 cạnh tương ứng)
t/g CBD = t/g FBD (c.g.c)
=> CD = FD (...)
t/g CDH = t/g FDH ( cạnh góc vuông và cạnh huyền)
=> CDH = FDH (...)
Có: CDH + CDE + EDB = 180o
Mà CDH = ADB ( đối đỉnh)
= FDH = EDB
Do đó, CDH + CDE + HDF = 180o
=> EDF = 180o
=> E, D, F thẳng hàng (đpcm)