Cho tam giác ABC.Trên tia đối của các tia CB;AC;BA lần lượt lấy các điểm A1;B1;C1 sao cho CA1=AB1=BC1 .Chứng minh rằng nêu A1B1C1 là tam giác đều thì tam giác ABC cũng là tam giác đều .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


XÉT TAM GIÁC ABD VÀ TAM GIÁC ACE CÓ
AB=AC (GT)
BD=CE (GT)
GÓC \(\widehat{ABD}+\widehat{_{ }_{ }B_1}=180^o\)
\(\widehat{ACE}+C_1=180^o\)
=>\(\hept{\begin{cases}\widehat{ABD}+B_1=\widehat{ACE}+\widehat{C}_1\\\widehat{B}_1=\widehat{C_1}\end{cases}}\hept{ }=>\widehat{ABD}=\widehat{ACE}\)
=>\(\Delta ABD=\Delta ACE\left(CGC\right)\)
=>\(AD=AE=>\Delta ADE\)CÂN TẠI A

a) xét tam giác ABC và tam giác DMC có:
CA=CD
góc ACB= góc DCM ( đối đỉnh)
BC=CM
=> tam giác ABC=tam giác DMC (c.g.c)
b) theo a) tam giác ABC=tam giác DMC=> góc A= góc D
mà đây là 2 góc so le trong nên MD//AB
c) Xét tam giác ICB và tam giác NCM có:
góc B= góc M ( tam giác ABC= tam giác DMC)
BC=MC
góc ICB= góc NCM ( đối đỉnh)
=> tam giác ICB= tam giác NCM( g.c.g)
=> IB=MN
Mà AB=MD ( tam giác ABC= tam giác DMC)
=> AB-IB= MD-MN
=> AI=ND

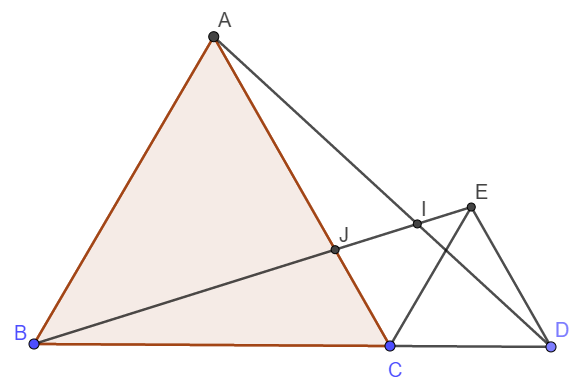
a) Do EC// AB nên \(\widehat{ECD}=\widehat{ABC}=60^o\)
Do ED// AC nên \(\widehat{EDC}=\widehat{ACB}=60^o\)
Xét tam giác ECD có \(\widehat{ECD}=\widehat{EDC}=60^o\Rightarrow\widehat{CED}=60^o\)
Suy ra ECD là tam giác đều.
b) Ta có :
\(\widehat{BCE}=\widehat{BCA}+\widehat{ACE}=60^o+\widehat{ACE}=\widehat{ECD}+\widehat{ACE}=\widehat{ACD}\)
Xét tam giác BCE và tam giác ACD có:
BC = AC (gt)
CD = CE (Do tam giác ECD đều)
\(\widehat{BCE}=\widehat{ACD}\) (cmt)
\(\Rightarrow\Delta BCE=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow BE=AC\)
c) Do \(\Delta BCE=\Delta ACD\Rightarrow\widehat{CBI}=\widehat{CAI}\)
Vậy thì \(\widehat{CBJ}+\widehat{BJC}=\widehat{JAI}+\widehat{JAI}\)
\(\Rightarrow180^o-\left(\widehat{CBJ}+\widehat{BJC}\right)=180^o-\left(\widehat{JAI}+\widehat{JAI}\right)\)
\(\Rightarrow\widehat{AIJ}=\widehat{JCB}=60^o\)
\(\Rightarrow\widehat{BID}=180^o-60^o=120^o\) (Hai góc kề bù)
\(\Rightarrow\widehat{BID}=2\widehat{BAC}\)
A1 B1 C1 A B C x x' y y' z z'
Gọi \(\widehat{A};\widehat{B};\widehat{C}\) là các góc của tam giác ABC. Kí hiệu các số đo góc x;y;z;x';y';z' nhưng hình vẽ trên.
Giả sử \(A_1B_1C_1\) là tam giác đều.
Không mất tính tổng quát, ta giả sử \(x\ge y\ge z\)
Xét các tam giác có hai cạnh tương ứng bằng nhau, ta có \(CB_1\ge AC_1\ge BA_1\)
hay \(CA\ge AB\ge BC\) (vì \(AB_1=BC_1=CA_1\))
Suy ra \(\widehat{B}\ge\widehat{C}\ge\widehat{A}\).(1)
Do tam giác \(A_1B_1C_1\) là tam giác đều nên \(x+x'=y+y'=z+z'\left(=60^o\right)\)
suy ra \(x'\le y'\le z'\)
Ta có: \(\widehat{A}=y+z'\ge z+x'=\widehat{B}\)(2)
Từ (1) và (2) suy ra \(\widehat{B}\ge\widehat{C}\ge\widehat{A}\ge\widehat{B}\), do đó \(\widehat{B}=\widehat{C}=\widehat{A}\)
Vậy tam giác ABC là tam giác đều.
Chúc bạn học tốt!!!