Cho \(\Delta ABC\) cân tại A có AB = 5cm; BC = 8cm. Kẻ \(AH\perp BC\) \(\left(H\in BC\right)\)
a, C/minh: HB = HC
b, Tính độ dài AH
c, Kẻ \(HD\perp AB;HE\perp AC\) . C/minh: \(\Delta HDE\) cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bn tự vẽ nha!!!
a,Xét ∆ABC và ∆ADC có
AB=AD (gt)
Góc BAC = góc DAC = 90°
AC : cạnh chug
=> ∆ABC = ∆ADC ( c.g.c)
=> góc ABC= góc ADC và góc BCA = góc DCA ( 2 góc tươg ứg ). (1)
=>Góc BAC= góc B + góc ACB và góc DAC = góc D + góc DCA. (2)
Mà góc B = Góc D. (3)
Từ (1),(2),(3)=> góc BCA+ góc DCA= 90° hay góc BCD=90°. (4)
Từ (4)=> ∆BCD là ∆ vuôg
b, ∆ABC = ∆ADC ( câu a)=> BC = CD = 5cm

Bài 2: Từ A kẻ H, từ B kẻ K
Suy ra: AB=HK=10cm
=> BH=KC=\(\frac{26-10}{2}=8\)cm
=> BH=8 và HC= 10+8=18
=> AH2= HB.HC=8.18 <=>AH= 12
=> S= \(\frac{10+26}{2}.12=216\) cm2
Bài 1: \(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Leftrightarrow BC=\sqrt{5^2+12^2}=13\)
Suy ra: BM=MC=BC/2=6,5
\(\Rightarrow MN^2=NC^2-MC^2\) (Tam giác MNC vuông tại M)
\(\Leftrightarrow MN=\sqrt{12^2-6,5^2}=\frac{\sqrt{407}}{2}\)

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>HB=HC
b: HB=HC=3cm
=>AH=4cm
AH là phân giác của góc BAC
=>góc BAH=góc CAH
c: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>HM=HN
=>ΔHMN cân tại H

Bài 1:
Gọi M là trung điểm của BC
Vẽ BE là tia phân giác của góc B, E thuộc AC
nối M với E
ta có: BM =CM = 1/2.BC ( tính chất trung điểm)
AB=1/2.BC (gt)
=> BM = CM= AB ( =1/2.BC)
Xét tam giác ABE và tam giác MBE
có: AB = MB (chứng minh trên)
góc ABE = góc MBE (gt)
BE là cạnh chung
\(\Rightarrow\Delta ABE=\Delta MBE\left(c-g-c\right)\)
=> góc BAE = góc BME = 90 độ ( 2 cạnh tương ứng)
=> góc BME = 90 độ
\(\Rightarrow BC\perp AM⋮M\)
Xét tam giác BEM vuông tại M và tam giác CEM vuông tại M
có: BM=CM(gt)
EM là cạnh chung
\(\Rightarrow\Delta BEM=\Delta CEM\left(cgv-cgv\right)\)
=> góc EBM = góc ECM ( 2 cạnh tương ứng)
mà góc EBM = góc ABE = 1/2. góc B (gt)
=> góc EBM = góc ABE = góc ECM
Xét tam giác ABC vuông tại A
có: \(\widehat{B}+\widehat{ECM}=90^0\) ( 2 góc phụ nhau)
=> góc EBM + góc ABE + góc ECM = 90 độ
=> góc ECM + góc ECM + góc ECM = 90 độ
=> 3.góc ECM = 90 độ
góc ECM = 90 độ : 3
góc ECM = 30 độ
=> góc C = 30 độ

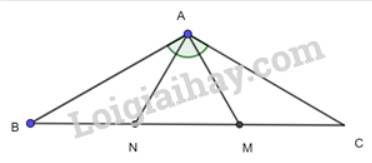
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.

\(cosABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}=\dfrac{1}{12}\)
=>góc ABC=85 độ
=>góc ABD=42,5 độ
Xet ΔBAC có BD làphân giác
=>DA/AB=DC/BC
=>DA/6=DC/1=30/7
=>DA=180/7cm
\(cosABD=\dfrac{BA^2+BD^2-AD^2}{2\cdot BA\cdot BD}\)
=>\(\dfrac{30^2+BD^2-\left(\dfrac{180}{7}\right)^2}{2\cdot30\cdot BD}=cos42.5\simeq0,74\)
=>BD^2-11700/49-44.4BD=0
=>\(BD\simeq49,25\left(cm\right)\)

\(AC=AD+DC=4+5=9\)
Ta có: \(AC^2=BC^2-AB^2\)
\(\to BC^2-AB^2=81\)
\(BD\) là đường phân giác \(\widehat{B}\)
\(\to\dfrac{BA}{AD}=\dfrac{BC}{DC}\)
\(\to\dfrac{BA}{4}=\dfrac{BC}{5}\)
\(\to\dfrac{BA^2}{16}=\dfrac{BC^2}{25}=\dfrac{BC^2-BA^2}{25-16}=\dfrac{81}{9}=9\)
\(\to\begin{cases}BA^2=144\\BC^2=225\end{cases}\)
\(\to\begin{cases}BA=12\\BC=15\end{cases}\)
Vậy \(BA=12cm, Bc=15cm\)