Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gợi ý: Kẻ AH ^ CD tại H, kẻ BK ^ CD tại K
Tính được SABCD = 180cm2
từ A hạ \(AE\perp DC\)
từ B hạ \(BF\perp DC\)
\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật
\(=>AB=EF=2cm\)
vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)
mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)
\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)
xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)
Đáp án A
Ta có: V = π A H 2 . A B + 1 3 π A H 2 B H + C K = 2 π A H 2 + 2 3 π A H 2
= 6 π ⇔ 2 A H 2 + 2 3 A H 2 = 6 ⇔ A H = 3 2 ⇒ S A B C D = A B + C D 2 . A H = 9 2
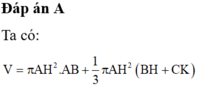
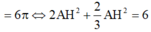
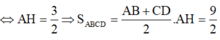
a)
Tam giác DAB có IO // AB nên
\(\frac{IO}{AB}=\frac{DI}{DA}\) (hệ quả của định lý Talet)
Tam giác ACD có OI // CD nên
\(\frac{OI}{CD}=\frac{AI}{AD}\) (hệ quả của định lý Talet)
Ta có: \(\frac{IO}{AB}+\frac{OI}{CD}=\frac{DI}{DA}+\frac{AI}{AD}=\frac{DI+AI}{DA}=\frac{DA}{DA}=1\)
=> \(OI\left(\frac{1}{AB}+\frac{1}{CD}\right)=1\)
=> \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{OI}\)
b)
Tam giác CAB có OK // AB nên
\(\frac{OK}{AB}=\frac{CK}{CB}\) (hệ quả của định lý Talet)
mà \(\frac{CK}{CB}=\frac{DI}{DA}\)
=> \(\frac{OK}{AB}=\frac{DI}{DA}\)
mà \(\frac{DI}{DA}=\frac{OI}{AB}\) (chứng minh trên)
=> \(\frac{OK}{AB}=\frac{OI}{AB}\)
=> OK = OI
mà \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{OI}\)
=> \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{OK}\)
c)
O là trung điểm của IK (OK = OI)
=> IK = 2OK
Ta có: \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{OK}\)
=> \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{2OK}\)
=> \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{IK}\)
Phương Linh P/s: Bạn có thể áp dụng định lý đã được chứng minh ở bài 19 SGK Toán 8 tập 2 trang 68.