Cho ∆ABC cân tại A, ( AB=AC= b; BC= a). Đường phân giác của ∆ABC có độ dài b. a) Chứng minh: 1𝑏−1𝑎=𝑏(𝑎+𝑏)2
b) Tính diện tích các tam giác ABD và ACD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

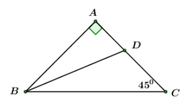
Vì tam giác ABC vuông cân tại
![]()
Vì BD là tia phân giác góc B
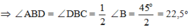
Xét ∆ ABD vuông tại A ta có:
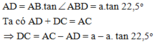
Đáp án cần chọn là: C

b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔABC có AK/AB=AH/AC
nên KH//CB

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔABM=ΔACM
b: góc NMC=góc ABC
=>góc NMC=góc NCM
=>ΔNMC cân tại N
c: Xét ΔCAB có
M là trung điểm của CB
MN//AB
=>N là trung điểm của AC
a, bạn viết rõ đề hơn được ko
b, Xét tam giác ABC cân tại A có AD là đường phân giác
nên AD đồng thời là đường trung tuyến => \(BD=DC=\frac{BC}{2}=\frac{a}{2}\)
AD đồng thời là đường cao
Xét tam giác ABD vuông tại D ta có :
\(S_{ABD}=\frac{1}{2}.AD.BD=\frac{1}{2}.b.\frac{a}{2}=\frac{ab}{4}\)(đvdt)
Xét tam giác ACD vuông tại D ta có :
\(S_{ACD}=\frac{1}{2}.AD.BD=\frac{ab}{4}\)(đvdt)
đề chỉ ghi thế nên mới hỏi.