Cho hình chữ nhật ABCD có AB=8cm;BC=6cm và hai đường chéo cắt nhau tại O .Qua B kẻ đường thẳng a vuông góc với BD , a cắt DC tại E
a, Chứng minh tam giác BCE và tam giác DBE đòng dạng
b, Kẻ đường cao CH của tam giác BCE Chứng minh BC2= CH.BD
c,Tính tỉ số diện tích của tam giác CEH và diện tích của tam giác DEB

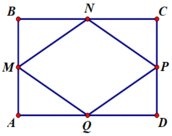
a) Xét \(\Delta BCE\) và \(\Delta DBE\) có :
\(\widehat{BED}:chung;\widehat{BDE}=\widehat{EBC}\) ( cùng phụ vơi \(\widehat{BEC}\) )
\(\Rightarrow\) \(\Delta BCE\) ~ \(\Delta DBE\)
b) Xét \(\Delta BCD\) và \(\Delta CHB\) có:
\(\widehat{BCD}=\widehat{BHC}=90^o;\widehat{BDC}=\widehat{CBH}\)
\(\Rightarrow\) \(\Delta BCD\) ~ \(\Delta CHB\)
\(\Rightarrow\frac{BC}{CH}=\frac{BD}{BC}\Rightarrow BC^2=CH.BD\)
\(\Rightarrow\) BD = \(\frac{BC^2}{BD}=\frac{6^2}{10}=3.6cm\)
c) BD = 10cm (áp dụng định lí Py tago )
Vì \(\Delta BCE\) ~ \(\Delta DBE\)
\(\Rightarrow\widehat{BCE}=\widehat{DBE}=90^o\)
Có : CH \(\perp\) BE ; DB \(\perp\) BE
\(\Rightarrow\) CH // BD
\(\Rightarrow\) \(\Delta ECH\sim\Delta EDB\)
\(\Rightarrow\) \(\frac{S\Delta CEH}{S\Delta DEB}=\frac{CH^2}{DB^2}=\frac{81}{625}\)
Thank bạn nhie