Câu 14. So sánh các cạnh của AABC biết rằng A= 75°;B = 50° :
А. АВ < АС < ВС В. ВС > АВ СА С. АВ 3 ВС СА D. AB < BC <CA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: a=40; b=60; c=80
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\)
nen BC<AC<AB
2: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{b}{\dfrac{1}{3}}=\dfrac{c}{\dfrac{1}{4}}=\dfrac{b+c}{\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{70}{\dfrac{7}{12}}=120\)
Do đó: b=40; c=30
Xét ΔABC có \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB

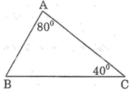
Ta có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠B = 180o - (∠A + ∠C )
= 180o - (80o + 40o) = 60o
Trong ΔABC, ta có: ∠A > ∠B > ∠C
Suy ra: BC > AC > AB (đối diện với góc lớn hơn là cạnh lớn hơn).

a: AC=16cm
XétΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAD cân tại B
c: Xét ΔBAC và ΔBDC có
BA=BD
\(\widehat{ABC}=\widehat{DBC}\)
BC chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)
Do đó: ΔBCD vuông tại D
a: AC=16cm
XétΔABC có AB<AC<BC
nên ˆC<ˆB<ˆAC^<B^<A^
b: Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAD cân tại B
c: Xét ΔBAC và ΔBDC có
BA=BD
ˆABC=ˆDBCABC^=DBC^
BC chung
Do đó: ΔBAC=ΔBDC
Suy ra: ˆBAC=ˆBDC=900BAC^=BDC^=900
Do đó: ΔBCD vuông tại D

\(\Delta ABC:\widehat{B}=50^o;\widehat{A}=70^o;\widehat{C}=180^o-\left(50^o+70^o\right)=60^o\\ Vậy:\widehat{B}< \widehat{C}< \widehat{A}\Rightarrow AC< AB< BC\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{C}=60^o\)
\(\Rightarrow\widehat{\text{A}\text{ }}>\widehat{C}>\widehat{B}\)
\(\Rightarrow BC>AB>AC\)

\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(Tổng ba góc trong một tam giác)
\(\Rightarrow\widehat{C}=180^o-\left(\widehat{A}+\widehat{B}\right)=180^o-\left(50^o+70^o\right)=60^o\)
\(\widehat{B}< \widehat{C}< \widehat{A}\left(50^o< 60^o< 70^o\right)\)
\(\Rightarrow AC< AB< BC\)(Tương ứng)

Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

ВС > АВ> СА
B