cho tam giác ABC có AM vuông góc BM; AN vuông góc BN, B1= B2=\(\dfrac{1}{2}\) ABC. Chứng minh: tam giác MAB đồng dạng tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


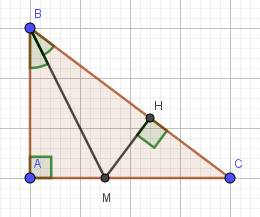
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)

a: Xét ΔABM vuông tại A và ΔHBM vuông tại H có
BM chung
\(\widehat{ABM}=\widehat{HBM}\)
Do đó: ΔABM=ΔHBM
b: Ta có: ΔABM=ΔHBM
nên AM=HM
mà HM<CM
nên AM<CM
c:
Ta có: ΔBAM=ΔBHM
nên BA=BH
Xét ΔAME vuông tại A và ΔHMC vuông tại H có
MA=MH
\(\widehat{AME}=\widehat{HMC}\)
Do đó: ΔAME=ΔHMC
Suy ra: ME=MC và AE=HC
Ta có: BA+AE=BE
BH+HC=BC
mà BA=BH
và AE=HC
nên BE=BC
Ta có: BE=BC
nên B nằm trên đường trung trực của EC\(\left(1\right)\)
Ta có: ME=MC
nên M nằm trên đường trung trực của EC\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BM là đường trung trực của EC
hay BM\(\perp\)EC
a) Xét △ ABM và △ HBM có:
\(\widehat{BAM}=\widehat{BHM}=90^0\)
BM chung
\(\widehat{ABM}=\widehat{HBM}\) ( BM phân giác của \(\widehat{B}\) )
⇒ △ ABM = △ HBM ( ch - gn )
b) Vì △ ABM = △ HBM ( cmt )
⇒ AM = HM ( 2 cạnh tương ứng )
△ AME = ▲ CMH ( g - c - g )
⇒ AM = CM ( 2 cạnh tương ứng )
c) Gọi N là giao điểm của BM và CE
Cm △ EBN = △ CBN ( c - g - c ) ( tự chứng minh nha, mik mệt quá )
⇒ \(\widehat{ENB}=\widehat{CNB}\) ( 2 góc tương ứng )
mà \(\widehat{ENB}=\widehat{CNB}=180^0\) ( kề bù )
⇒ BN ⊥ CE
⇒ BM ⊥ CE ( M ∈ BN )

a. Ta có: AB = AC
\(\Rightarrow\Delta ABC\) cân tại A.
Mà tia phân giác của góc cân đồng thời cắt cạnh đối tại trung điểm của nó.
Vậy: BM = MC.
b. Xét 2\(\Delta\): \(\Delta ABM\) và \(\Delta ACM\) có:
\(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\\widehat{BAM}=\widehat{CAM}\left(gt\right)\\AM.chung\end{matrix}\right.\)
\(\Rightarrow\) \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Vậy \(\widehat{AMB}=\widehat{AMC}\)
Mà: \(\widehat{BMC}=180^o\)
Vậy: \(\widehat{AMB}=90^o\) hay \(AM\perp BC\)
a) Xét tam giác ABM và tam giác ACM, ta có:
AB = AC (gt)
AM: cạnh chung
Góc BAM = góc CAM (do AM là tia phân giác của góc BAC)
=> tam giác ABM = tam giác ACM (c.g.c)
=> BM = MC (2 cạnh tương ứng) (đpcm)
b) Xét tam giác ABC, ta có:
AB = AC (gt)
=> tam giác ABC cân tại A
Mà AM là tia phân giác góc BAC
=> AM cũng là đường cao ứng với BC
=> AM vuông góc BC (đpcm)

a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay BM=CM
b: Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có
MB=MC
MH=MK
Do đó: ΔBHM=ΔCKM
Tham khảo:
a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay BM=CM
b: Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
ˆHAM=ˆKAMHAM^=KAM^
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
d: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có
MB=MC
MH=MK
Do đó: ΔBHM=ΔCKM

Xét ΔABM và ΔACN co
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
=>góc M=góc N
Xét ΔBME vuông tại E và ΔCNF vuông tại F có
BM=CN
góc M=góc N
Do đó: ΔBME=ΔCNF

a: Xét ΔANC vuông tại N và ΔAMB vuông tại M có
góc NAC chung
=>ΔANC đồng dạng với ΔAMB
=>AN/AM=AC/AB
=>AN*AB=AM*AC
b: AK vuông góc BM thì K trùng với M rồi bạn
