Cho hình vẽ. Biết MN // BC; AM =4cm, MB=8cm, BC=36cm. Tính độ dài đoạn thẳng MN??
em cần đáp án gấp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho hình vẽ. Biết MN // BC; AM =4cm, MB=8cm, BC=36cm. Tính độ dài đoạn thẳng MN??
em cần đáp án gấp ạ


- Áp dụng định lý talet vào tam giác ABC ( MN//BC ) ta được :
\(\dfrac{AB}{AN}=\dfrac{AC}{AM}=\dfrac{BC}{MN}=\dfrac{25}{10}=\dfrac{AC}{16}=\dfrac{45}{MN}\)
\(\Rightarrow\left\{{}\begin{matrix}AC=40\\MN=18\end{matrix}\right.\) ( đvđd )
Vậy ...
- Áp dụng định lý talet vào tam giác ABC ( MN//BC ) ta được :
AB/AN=AC/AM=BC/MN=25/10=AC/16=45/MN
⇒AC=40 ( đvđd )
MN =18 ( đvđd )
Vậy ...

Ta có: MN//BC ⇒ AM/ AB = AN/AC ⇔ 2/5 = 1,5/x ⇒ x = 3.75
Chọn đáp án C.

Ta có: MN//BC ⇒ AM/AB = AN/AC ⇔ 2/5 = 1,5/x ⇒ x = 5.1,5/2 = 3,75
Chọn đáp án C.

Ta có: MN // BC (gt), áp dụng hệ quả của định lý Ta – lét suy ra:
Suy ra: 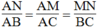 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)
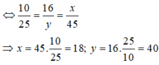


a, ∠ANM = ∠CBN (=90 độ) (chúng ở vị trí đồng vị)
=> MN//BC , theo hệ quả định lý Talet ta có:
AN/AB = MN/BC, cho AB=x (cm) thì AN = x-6 (cm)
Nên: (x-6)/x=1,5/6 => x=8(cm)
Nên AB = 8 cm
b, AD là đường phân giác của tam giác ABC nên:
AB/AC = BD/DC, nếu cho BD=x (cm) thì ta có DC=5-x (cm)
Nên: 4/6=x/(5-x) => 20=10x => x=2 (cm), nên BD= 2 cm
=> DC=3 cm
Theo hình vẽ ta có: AC//BE => ∠ACD = ∠DBE (so le trong)
Xét △BDE và △CDA có:
∠ACD=∠DBE (c/m tr)
∠ADC=∠BDE (đối đỉnh)
=> △BDE=△CDA (g.g)
=> BE/AC = BD/CD => BE/6=2/3 => BE=12:3=4 (cm)
Vậy: BD= 2 cm
BE= 4 cm
MN//BC
=>MN/BC=AM/AB
=>MN/36=1/3
=>MN=12cm