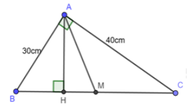
Cho tam giác ABC vuông tại A,đg cao AH,trung tuyến AM.Biết AH=40cm;AM=41cm.Tính tỉ số độ dài AB,AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BH = 18 cm ; MH = 7 cm ; MC = 25 cm ; AH = 24 cm. Chỉ có đáp án thôi nha!

Áp dụng định lý Pytago cho ABH vuông tại A có:

Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
Vì AM là đường trung tuyến M là trung điểm BC
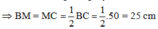
Ta có: MH = BM – BH = 25 – 18 = 7 cm
Đáp án cần chọn là: A

a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
nên BC=50(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB^2=BH\cdot BC\)
hay BH=18(cm)
Ta có: ΔBAC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên \(MB=MC=\dfrac{BC}{2}=25\left(cm\right)\)

A B C N S H P M D
Dễ thấy D nằm giữa M và H
Ta có : AD là tia phân giác góc BAC \(\Rightarrow\widehat{PAB}=\widehat{PAC}=\frac{1}{2}\widehat{BAC}=45^o\)
Mà \(\widehat{BAP}=\frac{1}{2}sđ\widebat{BP}=45^o\); \(\widehat{PAC}=\frac{1}{2}sđ\widebat{PC}=45^o\)
\(\Rightarrow sđ\widebat{BP}=sđ\widebat{PC}=90^o\)
Ta có : AM là đường trung tuyến nên M là tâm đường tròn ngoại tiếp tam giác ABC
\(\Rightarrow\widehat{BMP}=sđ\widebat{BP}=90^o\)
\(\Rightarrow BM\perp MP\)hay \(BC\perp MP\)( 1 )
Mà AH là đường cao tam giác ABC nên \(BC\perp AH\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra AH // MP