Một bảng hình chữ nhật ABCD có AB = 2013 cm; AD = 2014 cm. Một con kiến xuất phát từ điểm A, đi theo đường chéo mỗi ô vuông có cạnh 1cm (như hình dưới). Hỏi rằng sau khi đi qua tất cả các ô vuông mà mỗi ô chỉ đi qua một đường chéo thì con kiến có thể đến điểm nào trong 3 điểm B; C; D ? Tại sao?


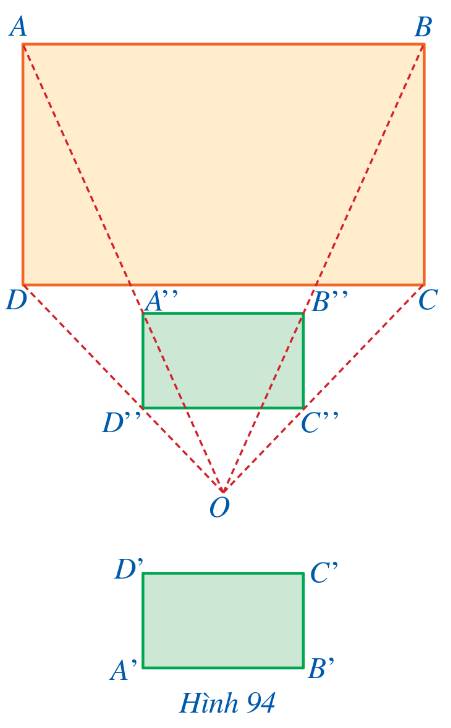
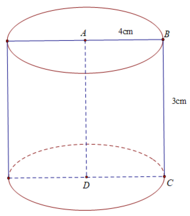
Bài này thì chắc là điểm D