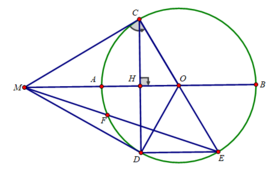
Cho AB=2R. Từ B kẻ tia Bx vuông góc với AB, Trên tia Bx lấy o sao cho OB=R. Vẽ đường tròn(O;R). Tia AO cắt (O) tại D và E (D nằm giữa A và E). Dựng đường tròn(A;AD) cắt AB tại C
a) C/M \(DE^2=AE\cdot AD\\ AC^2=AB\cdot BC\)
b) Tia BD cắt (A) tại P; một đường thẳng qua D cắt (A) tại M, cắt (O) tại N. C/M tg DPM đồng dạng tg DBN


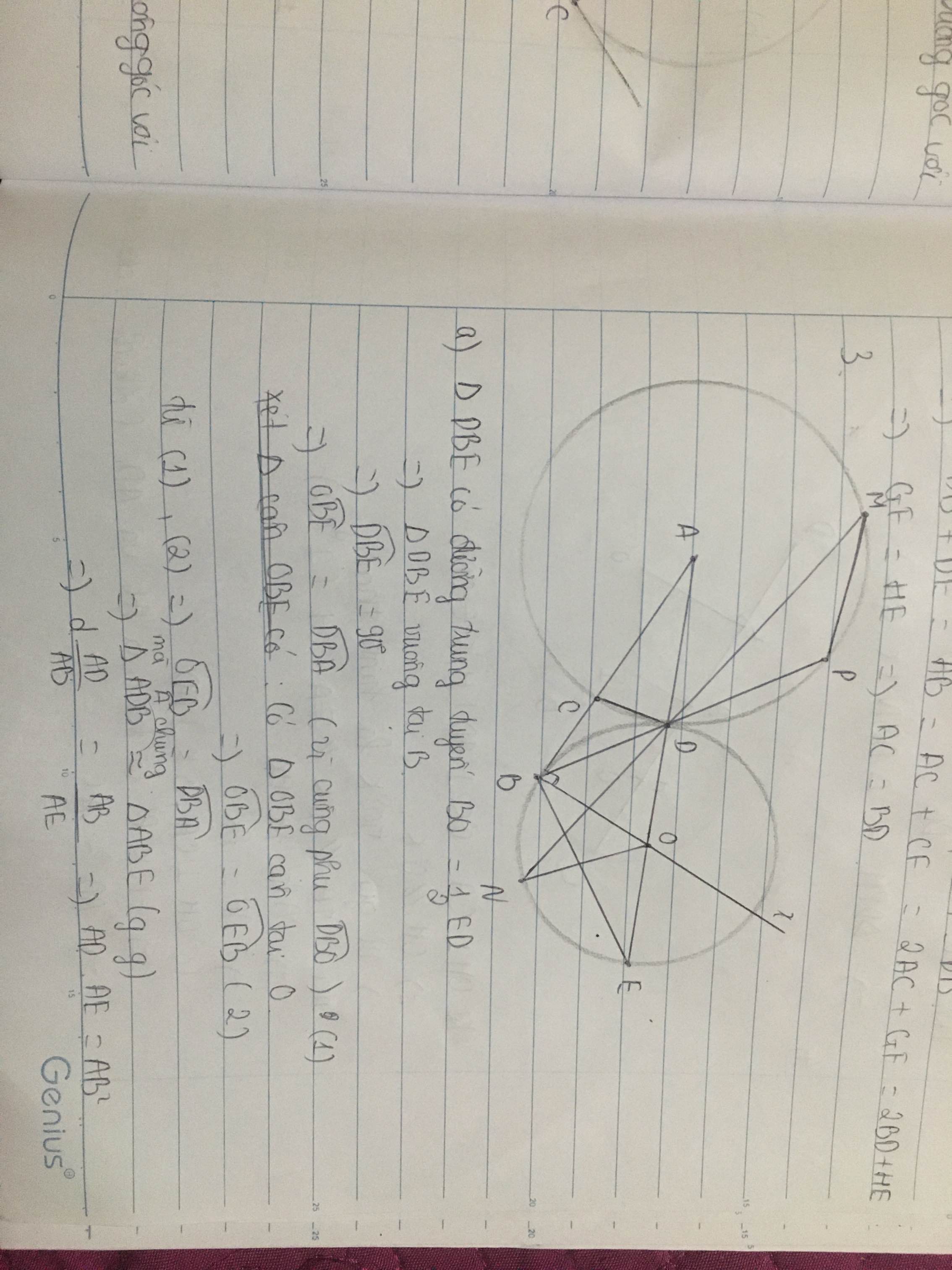

a) Xét \(\Delta ABD\) và \(\Delta ABE\) có:
\(\widehat{BAE}\) chung; \(\widehat{ABD}=\widehat{OBE}\) (cùng phụ với \(\widehat{OBD}\))
\(\Rightarrow\Delta ABD\infty\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\left(1\right)\Leftrightarrow AB^2=AE.AD\)
mà \(AB=DE\left(=2R\right)\) \(\Rightarrow DE^2=AE.AD\left(đpcm\right)\)
(1) \(\Leftrightarrow\dfrac{AE}{AB}=\dfrac{AB}{AD}\) mà \(AD=AC;DE=AB\)
\(\Rightarrow\)\(\dfrac{AE}{AB}=\dfrac{AD+DE}{AB}=\dfrac{AC+AB}{AB}=\dfrac{AB}{AD}=\dfrac{AB}{AC}\)
\(\Leftrightarrow\dfrac{AC+AB}{AB}=\dfrac{AB}{AC}\)
\(\Leftrightarrow\dfrac{AC+AB-AB}{AB}=\dfrac{AB-AC}{AC}\) (t\c tỉ lệ thức)
\(\Leftrightarrow\dfrac{AC}{AB}=\dfrac{BC}{AC}\Leftrightarrow AC^2=AB.BC\)(đpcm)
b) Cần c\m \(\Delta ADP\infty\Delta ODB\left(g.g\right)\) , \(\Delta MAD\infty\Delta NOD\left(g.g\right)\)
rồi suy ra \(\dfrac{DP}{BD}=\dfrac{MD}{ND}\left(=\dfrac{AD}{OD}\right)\) và \(\widehat{MDP}=\widehat{NDB}\left(đđ\right)\) là xong!
Câu b còn dễ hơn câu a