trên nửa đường tròn tâm O, đường kính AB=2R , vẽ dây BD=Rcăn2; AC cắt BD tại E
a.chứng minh EC.EA=ED.EB
b.tính số đo góc AEB
c.tính diện tích phần nửa đường tròn O nằm ngoài tứ giác ABDC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 7 2023
a: góc ADB=1/2*sđ cung AB=90 độ
=>AD vuông góc MB
Xét (O) có
MA,MC là tiếp tuyến
=>MA=MC
mà OA=OC
nên OM là trung trực của AC
=>OM vuông góc AC tại E
góc AEM=góc ADM=90 độ
=>AEDM nội tiếp
b: Xét ΔMAB vuông tại A có AD vuông góc MB
nên MA^2=MD*MB
19 tháng 12 2021
Cho nửa đường tròn đấy ạ . Mn giúp mk với , mk cảm ơn trước ạ 😊😊
12 tháng 12 2023
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C có \(sinCAB=\dfrac{CB}{AB}\)
=>\(\dfrac{CB}{2R}=sin30=\dfrac{1}{2}\)
=>CB=R
Xét ΔCAB vuông tại C có \(CB^2+CA^2=AB^2\)
=>\(CA^2+R^2=\left(2R\right)^2=4R^2\)
=>\(CA^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Chu vi tam giác ABC là:
\(C_{ABC}=CA+CB+AB=R+2R+R\sqrt{3}=R\left(3+\sqrt{3}\right)\)
b: Xét ΔCHA vuông tại H có \(sinCAH=\dfrac{CH}{CA}\)
=>\(\dfrac{CH}{R\sqrt{3}}=sin30=\dfrac{1}{2}\)
=>\(CH=\dfrac{R\sqrt{3}}{2}\)
Ta có: DA=2CH
=>\(DA=2\cdot\dfrac{R\sqrt{3}}{2}=R\sqrt{3}\)
Ta có: \(\widehat{DAC}+\widehat{CAB}=90^0\)
=>\(\widehat{DAC}=90^0-\widehat{CAB}=90^0-30^0=60^0\)
Xét ΔADC có \(AD=AC\left(=R\sqrt{3}\right)\) và \(\widehat{DAC}=60^0\)
nên ΔADC đều
=>\(\widehat{D}=60^0\)
Xét ΔOAC có OA=OC
nên ΔOAC cân tại O
=>\(\widehat{AOC}=180^0-2\cdot\widehat{OAC}=180^0-2\cdot30^0=120^0\)
c: Xét tứ giác DAOC có \(\widehat{DAO}+\widehat{DCO}+\widehat{ADC}+\widehat{AOC}=360^0\)
=>\(\widehat{DCO}+90^0+120^0+60^0=360^0\)
=>\(\widehat{DCO}=90^0\)
=>CD là tiếp tuyến của (O)
CM
3 tháng 12 2018
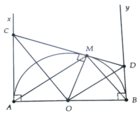
a, HS tự chứng minh
b, ΔCOD và ΔAMB đồng dạng => MC.MD = O M 2
c, AC = R 3
BD.AC = MC.MD = O M 2
=> BD = R 3 3
ai giúp mình nha !!
c đâu ra ???