Cho tam giác ABC có ABC = 70 độ;ACB = 30 độ . Trên nửa mặt phẳng bờ AC,
không chứa B vẽ đường thẳng thẳng AD song song với BC. Tính số đo các góc A1 và 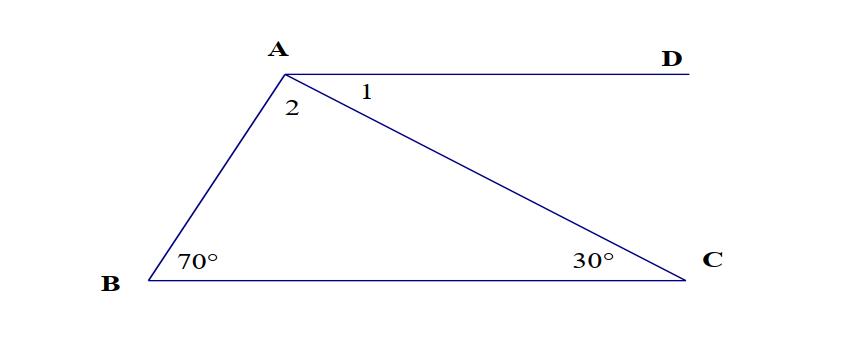 A2.
A2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho tam giác abc có góc a bằng 70 độ góc b bằng 55 độ tam giác abc có phải tam giác cân không vì sao

tam giác ABC tam giác cân vì có góc b và góc c bằng nhau vì a+b+c=180 độ
=> c=180-55-70=55
=>b=c
\(\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-70^0-55^0=55^0\)
Ta thấy \(\widehat{B}=\widehat{C}\left(=55^0\right)\)
Nên tam giác ABC cân tại A

\(\widehat{D}=180^0-\widehat{E}-\widehat{F}=50^0=\widehat{A}\\ \left\{{}\begin{matrix}AB=DE\\\widehat{A}=\widehat{D}\\AC=DE\end{matrix}\right.\Rightarrow\Delta ABC=\Delta DEF\left(c.g.c\right)\)

Vì tam giác ABC cân A nên góc B = góc C = 70
Góc A + góc B + góc C = 180° ( tổng 3 góc trong tam giác)
=> Góc A = 180 - 70 x 2 = 40°

* Theo mình thì phần a) Góc A = 90 độ sẽ hợp lý hơn chứ. Vậy nên mình sẽ làm theo cả hai góc A 90 độ và 80 độ nhé ( Nhưng bài của mình phần b) sẽ theo góc A = 90 độ )
a)
Góc A = 80 độ thì sẽ có thể tam giác ABC là tam giác cân, tam giác ⊥ tại B hoặc C, tam giác ABC là tam giác tù hoặc tam giác nhọn
Góc A = 90 độ thì tam giác ABC là tam giác vuông tại A
b)
Theo phần a), ta có: Tam giác ABC cân tại A
=> Góc B = góc C = ( 180 độ - 70 độ ) : 2 = 55 độ

Xét t/giác DEF có \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\) (tổng 3 góc của 1 t/giác)
=> \(\widehat{D}=180^0-\widehat{E}-\widehat{F}=180^0-70^0-60^0=50^0\)
Xét t/giác ABC và t/giác DEF
có: AB = DE (gt)
AC = DF (gt)
\(\widehat{A}=\widehat{D}=50^0\)
=> t/giác ABC = t/giác DEF (c.g.c)


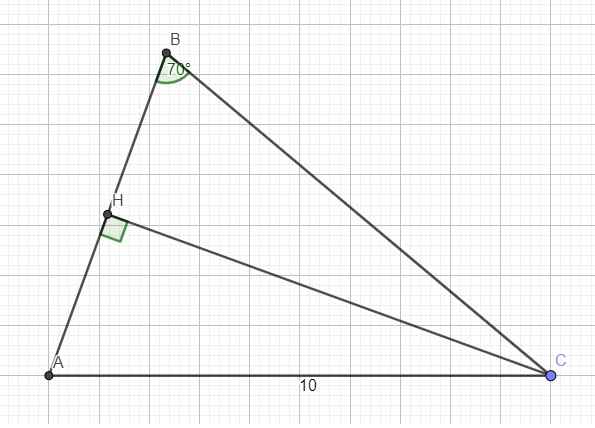
\(A=180^0-\left(B+C\right)=70^0\)
\(\Rightarrow A=B\Rightarrow\Delta ABC\) cân tại C
\(\Rightarrow BC=AC=10\left(cm\right)\)
Kẻ đường cao CH \(\Rightarrow\) H đồng thời là trung điểm AB
Trong tam giác vuông ACH:
\(cosA=\dfrac{AH}{AC}\Rightarrow AH=AC.cosA=10.cos70^0\approx3,42\left(cm\right)\)
\(AB=2AH\approx6,84\left(cm\right)\)
b. Cũng trong tam giác vuông ACH:
\(sinA=\dfrac{CH}{AC}\Rightarrow CH=AC.sinA=10.sin70^0\approx9,4\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}CH.AB\approx32,15\left(cm^2\right)\)

A1 = 30 độ ( Vì nó so e trong với acb và AD // BC )
A2 = 80 độ ( Tổng 3 góc trong tam giác nha bạn )
Ta có: AD//BC
\(\Rightarrow\widehat{A_1}=\widehat{ACB}=30^0\)(so le trong)
Ta có: AD//BC
\(\Rightarrow\widehat{ABC}+\widehat{BAD}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{ABC}+\widehat{A_1}+\widehat{A_2}=180^0\)
\(\Rightarrow\widehat{A_2}=180^0-\widehat{ABC}-\widehat{A_1}=180^0-70^0-30^0=80^0\)