tam giác ABC có BC =7cm ;AC=2cm,độ dài (tính bằng cm) là một số tự nhiên lẽ.Tính độ dài AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2022
Xét tam giác ABC
Theo định lí cos
\(AC^2=AB^2+BC^2-2AB.BCcos45=25\Rightarrow AC=5cm\)
Chu vi tam giác ABC là
AC + AB + BC = 7 + 3\(\sqrt{3}\)+5 = 12 + 3\(\sqrt{3}\)cm
VT
0
12 tháng 10 2021
Ta có:ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=54^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin36^0\)
nên \(AB\simeq4,11\left(cm\right)\)
\(\Leftrightarrow AC\simeq5,67\left(cm\right)\)
CM
27 tháng 10 2019
Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất bằng 4,5 nên cạnh nhỏ nhất của △ A'B'C' tương ứng với cạnh AB nhỏ nhất của △ ABC
Giả sử A'B' là cạnh nhỏ nhất 'của Δ A'B'C'
Vì
△
A'B'C' đồng dạng
△
ABC nên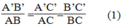 
Thay AB = 3(cm), AC = 7(cm), BC = 5(cm), A'B' = 4,5(cm) vào (1) ta có: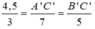 
Vậy: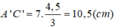 
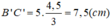
Áp dụng bất đẳng thức tam giác ta có:
\(BC+AC>AB>\left|BC-AB\right|\)
\(\Rightarrow7+2>BC>7-2\)
\(\Rightarrow9>BC>5\)
Vì BC là một số tự nhiên lẻ và thỏa mãn điều kiện trên \(\Rightarrow BC=7\left(cm\right)\)
Vậy: BC= 7 cm