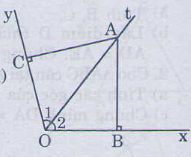
Cho \(\widehat{xOy}=120^o.\)Điểm A thuộc tia phân giác của góc đó. Kẻ \(AB\perp Ox\left(B\in Ox\right);AC\perp Oy\left(C\in Oy\right).CMR:\)
a) AB = AC
b) \(AO\perp BC\)
c) Kẻ BE vuông góc với phần kéo dài của Oy tại E. Cho OE = 3cm; OC = 5cm. Tính BC.
d) \(\Delta ABC\)là tam giác gì? Vì sao?

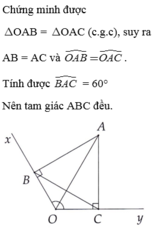
a) Ta thấy ngay (Cạnh huyền - góc nhọn)
b) Do
Mà AB = AC nên AO là đường trung trực đoạn thẳng BC hay AO vuông góc BC.
c) Do OB = OC nên OB = 5cm.
Áp dụng định lý Pi-ta-go cho tam giác vuông BEO ta có:
EC = EO + OC = 8cm
Vậy thì áp dụng định lý Pi-ta-go cho tam giác vuông BEC ta có:
d) Ta thấy ngay hay tam giác ABC là tam giác đều.