Cho tam giác ABC có ∠ A = 60 0 ; AB = 6cm, AC = 9cm. Dựng tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 1/3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2018
Xét \(\Delta ABC\)có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(\widehat{C}=40^o\)
Áp dụng bất đẳng thức trong tam giác ta có
AB<AC<BC ( 40o<600<800)
10 tháng 5 2018
Xét tam giác ABC, ta có:
\(\widehat{A}\) +\(\widehat{B}\) +\(\widehat{C}\) = 180 độ ( ĐL Pytago )
=> \(\widehat{C}\) = 180 -(\(\widehat{B}\) + \(\widehat{A}\) )
=180- (60+80) = 180 - 140 = 40độ
Xét tam giác ABC, ta có: \(\widehat{A}\) >\(\widehat{B}\) >\(\widehat{C}\) ( 80>60>40)
=> BC>AC>AB (t/c góc và cạnh đối diện trog tam giác)
23 tháng 7 2017
a) +Xét tam giác ABD :
ta có góc B = 60* ,góc BAD = 60*
mà góc B + góc BAD + ADB = 180* ( tổng 3 góc )
=> góc ADB = 60*
=> tam giac ABD là tam giác đều ( mỗi góc = 60*) => AB = BD = AD = 7cm
ta có H là trung diem BD => AH là duong trung tuyến,là tia phan giac goc BAD,là duong cao cùa tam giac ABD ( tam giac ABD đều ) => HD = HB = 1/2 BD = 3.5cm
+áp dụng định lí pitago vào tam giác ABH vuong tai H có AB = 7cm,BH = 3.5 cm :
AB^2 = AH^2 + BH^2 => em tự tính AH nhé
+ta có BH + HC = BC => HC = BC - HB = 15 - 3.5 = 11.5cm
+áp dụng dinh li pitago vào tam giac vuong AHC vuong tai H có AH ( lúc nãy tính ) và HC = 11.5cm
AC^2 =AH^2 + HC^2 => AC =13cm
b) AB ^2 + AC^2 có = BC ^2 ko? nếu = thì tam giac ABC vuong tai A
TN
2
23 tháng 9 2017
Giải phần góc nhé:
Gọi I là giao điểm của CE và BD.
Dễ thấy \(\Delta BEI\sim\Delta CDI\)
\(\Rightarrow\frac{EI}{DI}=\frac{BI}{CI}\)
\(\Rightarrow\frac{EI}{BI}=\frac{DI}{CI}=sin30^o=\frac{1}{2}\)
Bên cạnh đó có: \(\widehat{EID}=\widehat{BIC}\)
\(\Rightarrow\Delta EID\sim\Delta BIC\)
\(\Rightarrow\frac{ED}{BC}=\frac{EI}{BI}=\frac{DI}{CI}=\frac{1}{2}\)
\(\Rightarrow ED=MB=MC\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\)tam giác BDM đều
23 tháng 9 2017
Tam giác CEB vuông tại E có M là trung điểm cạnh huyền.
\(\Rightarrow ME=MB=MC\left(1\right)\)
Tam giác CDB vuông tại E có M là trung điểm cạnh huyền.
\(\Rightarrow MD=MB=MC\left(2\right)\)
Từ (1) và (2) \(\Rightarrow MD=ME\left(3\right)\)
Tam giác AEC vuông tại E
\(\Rightarrow\widehat{ACE}=90^o-\widehat{CAE}=90^o-60^o=30^o\)
Dễ thấy tứ giác EDCB nội tiếp đường tròn tâm M.
\(\Rightarrow\widehat{EMD}=2\widehat{ECD}=2.30^o=60^o\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\Delta BDM\) đều.
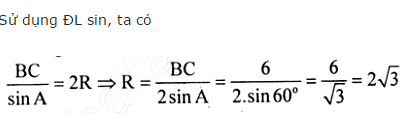
* Cách dựng:
- Trên cạnh AB dựng điểm B' sao cho = 2 cm
- Trên cạnh AC dựng điểm C' sao cho AC' = 3cm
- Nối B'C'
Khi đó AB'C' là tam giác cần dựng
* Chứng minh:
Theo cách dựng, ta có:
Suy ra: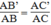
Lại có: ∠ A chung
Vậy △ AB'C' đồng dạng △ ABC (c.g.c)