Cho tam giác Abc có \(\widehat{A}=80^o;AB=AC\).Gọi M là trung điểm của BC.Tính các góc của tam giác AMB và \(\Delta AMC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
15 tháng 10 2017
a)
A B C 100*
=> Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o
100o + \(\widehat{B}+\widehat{C}\) = 180o
\(\widehat{B}+\widehat{C}\) = 180o - 100o
\(\widehat{B}+\widehat{C}\) = 80o
Góc B = (80o+50o):2 = 65o
=> \(\widehat{C}\) = 65o - 50o = 15o
Vậy \(\widehat{B}\) = 65o ; \(\widehat{C}\) = 15o
b)
80* A B C
Ta có : \(\widehat{3A}+\widehat{B}+\widehat{2C}\) = 180o
\(\widehat{3A}+\widehat{2C}\) = 180o - 80o
\(\widehat{3A}+\widehat{2C}\) = 100o
=> \(\widehat{A}\) = 100o:(3+2).3 = 60o
\(\widehat{C}\) = 100o - 60o = 40o
Vậy \(\widehat{A}\) = 60o ; \(\widehat{C}\) = 40o
5 tháng 2 2022
B A C 80 I ? 10 30
Do ΔABC cân tại B => A = C = \(\dfrac{180^o-80^o}{2}=50^o\)
=> góc BAI = 50o - 10o = 40o
góc BCI = 50o - 30o = 20o
=> \(IBC=\dfrac{1}{3}ABI\Rightarrow IBC=\dfrac{80^o}{3+1}=20^o;ABI=80^o-20^o=60^o\)
\(\Leftrightarrow AIB=180^o-40^o-60^o=80^o\)
HN
1
11 tháng 7 2019
Ta có: \(\widehat{A}=\frac{q}{3}\widehat{C}\).
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+80^o+\widehat{C}=180^o\)
=> \(\frac{q}{3}\widehat{C}+\widehat{C}=180^o-80^o=100^o\)
=> \(\widehat{C}\left(q+3\right)=300^o\)
=> \(\widehat{C}=\frac{300^o}{q+3}\)
=> \(\widehat{A}=\frac{q}{3}.\frac{300^o}{q+3}=\frac{100^oq}{q+3}\)
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
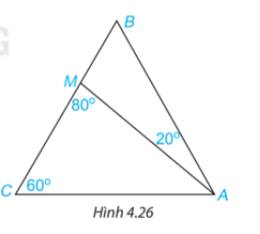
Ta có:
\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)
Áp dụng định lí tổng ba góc trong một tam giác:
+) Trong tam giác AMB có:
\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)
+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)
7 tháng 1 2018
B C A M O
\(\Delta ABC\)cân tại A, \(\widehat{A}=80^o\)suy ra : \(\widehat{B}=\widehat{C}=50^o\)
Vẽ tam giác BCM đều ( M và A thuộc cùng một nửa mặt phẳng bờ BC )
\(\widehat{MCA}=60^o-50^o=10^o\)
\(\Delta AMB=\Delta AMC\)( c.c.c )
suy ra : \(\widehat{AMB}=\widehat{AMC}=60^o:2=30^o\)
\(\Delta OBC=\Delta AMC\)( g.c.g ) suy ra CO = CA do đó \(\Delta COA\)cân
5 tháng 7 2021
Có \(\widehat{B}=180^0-105^0-30^0=45^0\)
Kẻ AH vuông góc với BC
\(\Rightarrow\Delta ABH\) là tam giác vuông cân tại A
\(\Rightarrow AH=BH\)
Có \(tanC=\dfrac{AH}{HC}\Leftrightarrow HC=\dfrac{AH}{tan30^0}=\sqrt{3}AH\)
\(\Rightarrow BH+CH=AH+\sqrt{3}AH\Leftrightarrow BC=\left(1+\sqrt{3}\right)AH\)\(\Leftrightarrow AH=\dfrac{BC}{1+\sqrt{3}}=\dfrac{2}{1+\sqrt{3}}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{2}{1+\sqrt{3}}.2=\dfrac{2}{1+\sqrt{3}}\) (cm2)
Vậy...
22 tháng 2 2020
Câu hỏi của Nguyễn Vũ Thu Hương - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo!
A B C M
Xét t/g AMB và t/g AMC có:
AB = AC (gt)
MB = MC (vì M là trung điểm của BC)
AM là cạnh chung
=> t/g AMB = t/g AMC (c-c-c)
=> góc BAM = góc CAM ; góc ABM = góc ACM ; góc AMB = góc AMC
Do góc A = 80 độ => góc BAM = góc CAM = 40 độ
góc AMB + góc AMC = 180 độ (kề bù) mà góc AMB = góc AMC => góc AMB = góc AMC = 90 độ
góc BAM + góc AMB + góc ABM = 180 độ => góc AMB = góc AMC = 50 độ
Vậy...