Trong không gian với hệ tọa độ Oxyz, cho A ( 1;0;5 ) và B ( 2;2;6 ) và đường thẳng ∆ = x 1 = y + 2 2 = z - 4 1 và mặt phẳng (a): 2x +y - z + 3 = 0 . Tìm điểm M nằm trên mặt phẳng (a) sao cho MB = 6 2 và A B M ^ = 60 o .
A. M 1 ; 3 2 ; 13 2
B. M ( 0;0;3 )
C. M ( 1;1;6 )
D. M 1 2 ; 2 ; 6

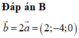

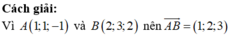

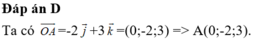
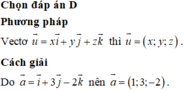
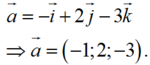
Ta thấy và
và  .
.
Áp dụng định lý hàm số Cosin cho tam giác MAB ta có:
M A 2 = B A 2 + B M 2 - 2 B A . B M cos 60 o = 6 + 3 2 - 2 6 . 6 2 . 1 2 = 9 2
Suy ra M A = 3 2 2 . Từ đây ta nhận thấy A B 2 = M A 2 + M B 2 nên tam giác MAB vuông tại M và có M A B ^ = 30 o .
Mặt khác:
sin ∆ ^ ; a = 2 + 2 - 1 6 . 6 = 1 2 ⇒ ∆ ^ ; a = 30 o = M A B ^ .
Từ đó suy ra M chính là hình chiếu của B lên mặt phẳng (a).
Khi đó M B : x - 2 2 = y - 2 1 = z - 6 - 1
nên M ( 2m + 2; m + 2; -m + 6 )
Vì M thuộc mặt phẳng (a) nên
2( 2m + 2 ) + ( m + 2 ) - ( -m + 6 ) + 3 = 0 ⇒ m = - 1 2
Vậy M 1 ; 3 2 ; 13 2
Đáp án A