Trong không gian tọa độ Oxyz cho các điểm A(1;5;0), B(3;3;6) và đường thẳng Δ: x + 1 2 = y - 1 - 1 = z 2 . Gọi M(a;b;c) ∈ Δ sao cho chu vi tam giác MAB đạt giá trị nhỏ nhất. Tính tổng T=a+b+c?
A. T = 2.
B. T = 3
C. T = 4
D. T = 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A.
Phương pháp:
+) Cho hai điểm ![]()
Khi đó ta có: ![]()
Cách giải:
Ta có:
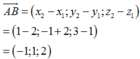

Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).

Chọn B.
Gọi B, C, D lần lượt là hình chiếu của A lên các trục Ox , Oy , Oz ⇒ B ( 1 ; 0 ; 0 ) C ( 0 ; - 1 ; 0 ) D ( 0 ; 0 ; 2 )
Suy ra phương trình mặt phẳng ( Q ) : x 1 + y - 1 + z 2 = 1 ⇔ 2 x - y + z - 2 = 0 .

Đáp án B
Phương pháp :
A
(
2
;
1
;
-
1
)
,
B
(
3
;
3
;
1
)
,
C
(
4
;
5
;
3
)
.
![]()
=> A, B, C thẳng hàng.