3x = y ; 5y = 4z và 6x+7y+8z= 456
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 4 2019
a) Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
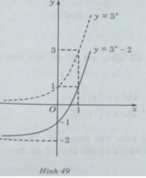
b) Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
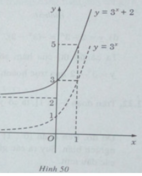
c)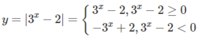 
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
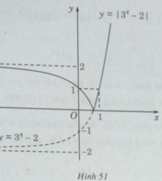
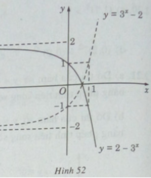
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).
1 tháng 12 2021
\(=\dfrac{3x-y+6x+4y}{3x+y}=\dfrac{9x+3y}{3x+y}=\dfrac{3\left(3x+y\right)}{3x+y}=3\)
TA
8 tháng 6 2021
PT của đường thẳng cần tìm có dạng: `(d): y=ax+b `
`(d)` vuông góc `(d') : y=1/3 x-7/3 <=> a. 1/3 = -1 <=> a=-3`
`=> y=-3x+b`
`A (0;4) \in (d) <=> 4=-3.0+b <=> b=4`
`=> y=-3a+4`.
AH
Akai Haruma
Giáo viên
22 tháng 2 2020
Lời giải:
Màu xanh lá: $y=3x$
Màu xanh nước biển: $y=-3x$
Màu đỏ: $y=\frac{x}{2}$
Màu cam: $y=\frac{-x}{3}$
MT
4
AH
Akai Haruma
Giáo viên
4 tháng 1 2021
Lời giải:Đồ thị xanh lá là $y=3x$
Đồ thị xanh dương là $y=-3x$
Đồ thị hồng là $y=\frac{1}{2}x$
Đồ thị cam là $y=-\frac{1}{3}x$
Cách vẽ đồ thị là bạn lấy 2 điểm thuộc đồ thị rồi nối với nhau. Ví dụ như đồ thị $y=-3x$ ta nối 2 điểm $(0;0)$ và $(1;-3)$
KV
5 tháng 1 2021
a) y = 3x
Cho x = 1 \(\Rightarrow\) y = 3 \(\Rightarrow\) A(1; 3)
Đồ thị:
BN
1
NB
2
LB
7 tháng 3 2018
Đặt \(t=3x+y\)
pt \(\Leftrightarrow t^3-3t^2+3t-1=-27\)
\(\Leftrightarrow\left(t-1\right)^3+3^3=0\)
\(\Leftrightarrow\left(t-1+3\right)\left(\left(t-1\right)^2-3\left(t-1\right)+9\right)=0\)
\(\Leftrightarrow\left(t+2\right)\left(t^2-5t+13\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t+2=0\\t^2-5t+13=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-2\\t^2-5t+13=0\left(vl\right)\end{matrix}\right.\)
\(\Leftrightarrow3x+y=-2\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2-3x\\x\in R\end{matrix}\right.\)
Theo bài ra ta có: \(6x+7y+8z=456\)
\(3x=y\Rightarrow\frac{x}{1}=\frac{y}{3}\Rightarrow\frac{x}{4}=\frac{y}{12}\left(1\right)\)
\(5y=4z\Rightarrow\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{y}{12}=\frac{z}{15}\left(2\right)\)
Từ (1) và (2) suy ra \(\frac{x}{4}=\frac{y}{12}=\frac{z}{15}\Rightarrow\frac{6x}{24}=\frac{7y}{84}=\frac{8z}{120}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{6x}{24}=\frac{7y}{84}=\frac{8z}{120}=\frac{6x+7y+8z}{24+84+120}=\frac{456}{228}=2\)
\(\Rightarrow\left\{\begin{matrix}\frac{6x}{24}=2\Rightarrow x=\frac{2\cdot24}{6}=8\\\frac{7y}{84}=2\Rightarrow y=\frac{2\cdot84}{7}=24\\\frac{8z}{120}=2\Rightarrow z=\frac{2\cdot120}{8}=30\end{matrix}\right.\)
Ta có:
3x = y => x = \(\frac{y}{3}\) => \(\frac{x}{4}\) = \(\frac{y}{12}\) (1)
5y = 4z => \(\frac{y}{4}\) = \(\frac{z}{5}\) => \(\frac{y}{12}\) = \(\frac{z}{15}\) (2)
Từ (1) và (2) suy ra \(\frac{x}{4}\) = \(\frac{y}{12}\) = \(\frac{z}{15}\)
=> \(\frac{6x}{24}\) = \(\frac{7y}{84}\) = \(\frac{8z}{120}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{6x}{24}\) = \(\frac{7y}{84}\) = \(\frac{8z}{120}\) = \(\frac{6x+7y+8z}{24+84+120}\) = 114
Do \(\frac{6x}{24}\) = 114 => x = .....
\(\frac{7y}{84}\) = 114 => y = .....
\(\frac{8z}{120}\) = 114 => z = ......
Vậy x = ...; y = ... và z = ...