Có bao nhiêu giá trị nguyên của tham số m ∈ [ − 5 ; 5 ] để hàm số y = x 4 + x 3 − 1 2 x 2 + m có 5 điểm cực trị?
A. 7
B. 5
C. 4
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
y = 3 x 4 - 4 x 3 - 12 x 2 + m = f x + m , f x = 3 x 4 - 4 x 3 - 12 x 2 f ' x = 12 x 3 - 12 x 2 - 24 x = 12 x x + 1 x - 2 y ' = f ' x f x + m f x + m = 0 ⇒ [ f ' x = 0 f x = - m
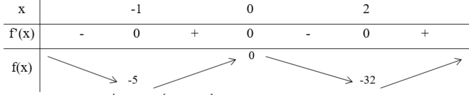 Dựa vào BBT ta thấy hàm số có 5 điểm cực trị khi và chỉ khi
Dựa vào BBT ta thấy hàm số có 5 điểm cực trị khi và chỉ khi
[ - m > 0 - 32 < - m ≤ - 5 ⇒ [ m < 0 5 ≤ m < 32 ⇒ m = 5 ; 6 ; . . . ; 31

Hàm số ![]() có 5 điểm cực trị khi và chỉ khi hàm số
có 5 điểm cực trị khi và chỉ khi hàm số ![]() có 2 cực trị nằm về hai phía của trục Ox.
có 2 cực trị nằm về hai phía của trục Ox.
Ta có:
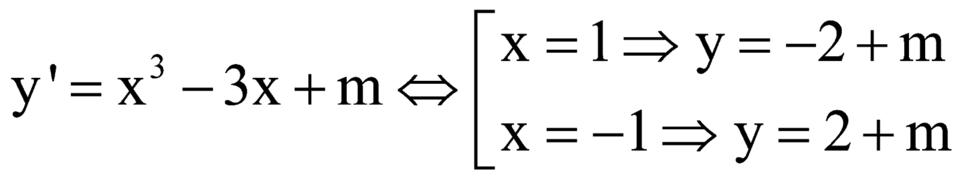
Hai điểm cực trị nằm về 2 phía trục Ox
![]()
Kết hợp điều kiện ![]() .
.
Vậy có 3 giá trị của m thỏa mãn ycbt.
Chọn B

Đáp án B.
Đặt f x = 3 x 4 - 4 x 3 - 12 x 2 → f ' x = 12 x 3 - 12 x 2 - 24 x ; ∀ x ∈ ℝ .
Khi đó y = f x + m ⇒ y ' = f ' x . f x + m f x + m . Phương trình y ' = 0 ⇔ [ f ' x = 0 f x = - m ( * ) .
Để hàm số đã cho có 7 điểm cực trị ⇔ y ' = 0 có 5 nghiệm phân biệt
Mà f ' x = 0 có 3 nghiệm phân biệt ⇒ f x = - m có 2 nghiệm phân biệt.
Dựa vào BBT hàm số f(x) để (*) có 2 nghiệm phân biệt ⇔ [ - m > 0 - 5 > - m > - 32 ⇔ [ m < 0 5 < m < 32 .
Kết hợp với m ∈ ℤ + suy ra có tất cả 27 giá trị nguyên cần tìm.

Đáp án B
y = 3 x 4 − 4 x 3 − 12 x 2 + m = f ( x ) + m , ( f ( x ) = 3 x 4 − 4 x 3 − 12 x 2 ) f ' ( x ) = 12 x 3 − 12 x 2 − 24 x = 12 x ( x + 1 ) ( x − 2 ) y ' = f ' ( x ) ( f ( x ) + m ) f ( x ) + m = 0 ⇒ f ' ( x ) = 0 f ( x ) = − m
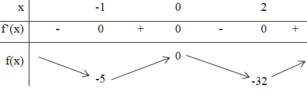
Dựa vào BBT ta thấy hàm số có 5 điểm cực trị khi và chỉ khi
− m > 0 − 32 < − m ≤ − 5 ⇒ m < 0 5 ≤ m < 32 ⇒ m = 5 ; 6 ; ...31
Đáp án D