Trong không gian Oxyz cho vecto a → = (1; −3; 4). Tìm y 0 và z 0 để cho vecto b → = (2; y 0 ; z 0 ) cùng phương với a →
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Vectơ b → cùng phương với vectơ a → khi và chỉ khi tồn tại một số thực k thỏa mãn:
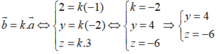

Đáp án C
Vì vectơ b → ngược hướng với vectơ a → và | b → | = 2| a → | nên:
b → = -2 a → = (-2; 4; -6)

Đáp án C
Ta có:
![]()
Mặt khác hai vectơ này cùng phương nên ta có:
![]()
Từ đó ta suy ra
![]()
Lưu ý. Đáp án D là sai, do sai lầm trong tính độ dài của vectơ a ⇀
![]()
Mà hai vectơ này cùng phương nên ta có:
![]()
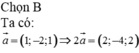
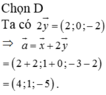


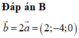
Ta biết rằng a → và b → cùng phương khi và chỉ khi a → = k b → với k là một số thực. Theo giả thiết ta có: b → = ( x 0 ; y 0 ; z 0 ) với x 0 = 2. Ta suy ra k = 1/2 nghĩa là l = x 0 /2
Do đó: −3 = y 0 /2 nên y 0 = -6
4 = z 0 /2 nên z 0 = 8
Vậy ta có b → = (2; −6; 8)