Trong không gian Oxyz, cho A(-1;3;-1), B(4;-2;4) và điểm M thay đổi trong không gian thỏa mãn 3MA=2MB. Giá trị lớn nhất của P=\(\left|2\overrightarrow{MA}-\overrightarrow{MB}\right|\)?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
PT
1

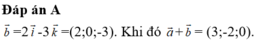
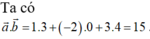
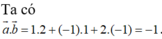
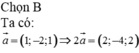
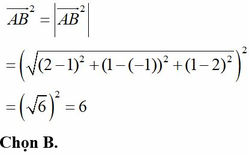
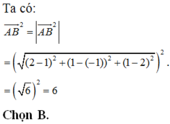
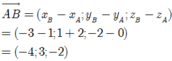
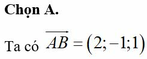
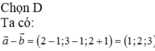
\(M\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-1-x;3-y;-1-z\right)\\\overrightarrow{MB}=\left(4-x;-2-y;4-z\right)\end{matrix}\right.\)
\(9MA^2=4MB^2\Leftrightarrow9\left(x+1\right)^2+9\left(y-3\right)^2+9\left(z+1\right)^2=4\left(x-4\right)^2+4\left(y+2\right)^2+4\left(z-4\right)^2\)
\(\Leftrightarrow\left(x+5\right)^2+\left(y-7\right)^2+\left(z+5\right)^2=108\)
\(2\overrightarrow{MA}-\overrightarrow{MB}=-\left(x+6;y-8;z+6\right)\)
Gọi \(\overrightarrow{u}=\left(x+5;y-7;z+5\right)\) ; \(\overrightarrow{v}=\left(1;-1;1\right)\)
Theo BĐT vecto ta có:
\(\left|\overrightarrow{u}+\overrightarrow{v}\right|\le\left|\overrightarrow{u}\right|+\left|\overrightarrow{v}\right|\Rightarrow P=\left|\overrightarrow{u}+\overrightarrow{v}\right|\le\sqrt{108}+\sqrt{3}=7\sqrt{3}\)