Giải Pt sau bằng pp cộng đại số:{x+2y=4;3x+3y=1}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 1 2022
\(\left\{{}\begin{matrix}x+y=3\\x+2y=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x+2=3\\y=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
17 tháng 1 2022
\(\left\{{}\begin{matrix}x+y=3\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
7 tháng 1 2018
a.\(\hept{\begin{cases}3x-2y=1\\2x+4y=3\end{cases}}\)
<=>\(\hept{\begin{cases}6x-4y=2\\2x+4y=3\end{cases}}\)
<=>\(\hept{\begin{cases}8x=5\\2x+4y=3\end{cases}}\)
<=>\(\hept{\begin{cases}x=\frac{5}{8}\\2\cdot\frac{5}{8}+4y=3\end{cases}}\)
<=>\(\hept{\begin{cases}x=\frac{5}{8}\\4y=\frac{7}{4}\end{cases}}\)
<=>\(\hept{\begin{cases}x=\frac{5}{8}\\y=\frac{7}{16}\end{cases}}\)
7 tháng 1 2018
a) \(\hept{\begin{cases}3x-2y=1\\2x+4y=3\end{cases}}\Rightarrow\hept{\begin{cases}6x-4y=2\\2x+4y=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}8x=5\\2x+4y=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{8}\\\frac{5}{4}+4y=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{5}{8}\\4y=\frac{7}{4}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{8}\\y=\frac{7}{16}\end{cases}}\)
vậy hpt có nghiệm duy nhất \(\left(x;y\right)=\left(\frac{5}{8};\frac{7}{16}\right)\)
b) \(\hept{\begin{cases}4x-3y=1\\-x+2y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}8x-6y=2\\-3x+6y=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}5x=5\\-3x+6y=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\-3+6y=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\)
vậy hpt có nghiệm duy nhất \(\left(x;y\right)=\left(1;1\right)\)
PD
8 tháng 8 2021
Đặt $|x-1|=a,\sqrt{y+2}=b(x\in \Bbb R, y\ge -2)$
$\Rightarrow \begin{cases}2a-b=4\\a+3b=9\end{cases}\\\Leftrightarrow \begin{cases}2a=b+4\\a+3b=9\end{cases}\\\Leftrightarrow \begin{cases}a=\dfrac{b+4}{2}\\a+3b=9\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\\dfrac{b+4}{2}+3b=9\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\b+4+6b=18\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\7b=14\end{cases}\\\Leftrightarrow\begin{cases}a=\dfrac{b+4}{2}\\b=2\end{cases}\\\Leftrightarrow\begin{cases}a=3\\b=2(TM)\end{cases}\\\Leftrightarrow\begin{cases}|x-1|=3\\\sqrt{y+2}=2\end{cases}\\\Leftrightarrow\begin{cases}\left[\begin{array}{1}x-1=3\\x-1=-3\end{array}\right.\\y+2=4\end{cases}\\\Leftrightarrow\begin{cases}\left[\begin{array}{1}x=4\\x=-2\end{array}\right.\\y=2(TM)\end{cases}$
Vậy $(x,y)=\{(4;2);(-2;2)\}$
14 tháng 6 2022
a: \(\left\{{}\begin{matrix}3x-2y=1\\2x+4y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-4y=2\\2x+4y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x=5\\3x-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{8}\\2y=3x-1=\dfrac{15}{8}-1=\dfrac{7}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{8}\\y=\dfrac{7}{16}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}4x-3y=1\\-x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-3y=1\\-4x+8y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=-1+2y=-1+2=1\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{2}{3}x+\dfrac{4}{3}y=1\\\dfrac{1}{2}x-\dfrac{3}{4}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=3\\2x-3y=8\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{41}{14}\\y=-\dfrac{5}{7}\end{matrix}\right.\)
CM
21 tháng 10 2018
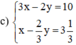(Nhân hai vế pt 2 với 3 để hệ số của y bằng nhau)
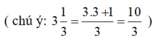
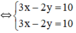(Trừ từng vế hai phương trình)
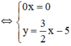
Phương trình 0x = 0 nghiệm đúng với mọi x.
Vậy hệ phương trình có vô số nghiệm dạng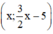 
(x ∈ R).
CM
13 tháng 9 2017
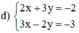
(Nhân hai vế pt 1 với 2, pt 2 với 3 để hệ số của y đối nhau)
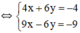(Hệ số của y đối nhau nên cộng từng vế hai phương trình).
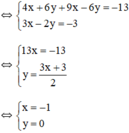
Vậy hệ phương trình có nghiệm duy nhất (-1; 0).
CM
3 tháng 1 2020
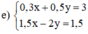(Nhân hai vế pt 1 với 4 để hệ số của y đối nhau)
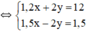(Hệ số của y đối nhau nên ta cộng từng vế 2pt)
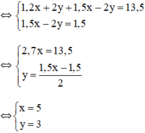
Vậy hệ phương trình có nghiệm duy nhất (5; 3).
CM
8 tháng 1 2019
(Các phần giải thích học sinh không phải trình bày).
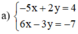(Nhân 2 vế pt 1 với 3; nhân pt 2 với 2 để hệ số của y đối nhau)
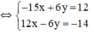(hệ số của y đối nhau nên ta cộng từ vế 2 pt)
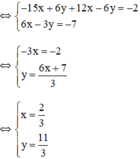
Vậy hệ phương trình có nghiệm duy nhất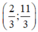 
Lời giải:
$x+2y=4$
$3x+3y=1$
$\Rightarrow 3(x+2y)-(3x+3y)=4.3-1$
$\Leftrightarrow 3y=11$
$\Leftrightarrow y=\frac{11}{3}$
$x=4-2y=4-2.\frac{11}{3}=\frac{-10}{3}$
Vậy......