Phương trình tham số của đường thẳng ∆ đi qua điểm M(2; 3) và có hệ số góc k = 4 là:
A.y = 4(x – 2) + 3
B. 4x – y – 5 = 0
C. x = 2 + t y = 3 + 4 t , t ∈ R
D. x = 2 + 2 t y = 3 + t , t ∈ R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: vecto AB=(-1;6)
=>VTPT là (6;1)
Phương trình tham số là;
x=1-t và y=-2+6t
b: PTTQ là:
6(x-1)+1(y+2)=0
=>6x-6+y+2=0
=>6x+y-4=0

Đáp án A
Do 2 đường thẳng d và (d’) vuông góc với nhau nên VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại.
Mà đường thẳng (d’) có VTPT là n → ( 1 ; 6 ) n ê n u → ( 1 ; 6 ) là VTCP của đường thẳng (d) .
Khi đó phương trình tham số của đường thẳng (d) cần tìm là:
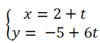

Do d \(\left\{{}\begin{matrix}điquaM\left(2;6\right)\\vtcp\overrightarrow{u}=\left(2;-3\right)\end{matrix}\right.\)
=> Pt tham số: \(\left\{{}\begin{matrix}x=2+2t\\y=6-3t\end{matrix}\right.\)

Chọn D
Phương pháp:
Phương trình tham số của đường thẳng đi qua điểm


Chọn D.
Phương pháp:
Phương trình tham số của đường thẳng đi qua điểm


ĐÁP ÁN B
Phương trình tham số của đường thẳng đi qua M (3; 4) và vecto chỉ phương u → ( 3 ; 4 ) là:
x = 3 + 3 t y = 4 + 4 t ( t ∈ R )
Hướng dẫn:
Đường thẳng ∆ có hệ số góc k = 4 nên có vectơ chỉ phương u → = 1 ; 4 . Do đó C là phương án đúng.
Chú ý. Học sinh có thể nhầm sang các loại phương trình khác của đường thẳng như các phương án ở A và B. Đây đều là phương trình của đường thẳng nhưng không là phương trình tham số.